23．(本小题满分9分)

已知⊙T与坐标轴有四个不同的交点M、P、N、Q，其中P是直线与轴的交点。点Q与点P关于原点对称。抛物线经过点M、P、N，其顶点为H。

(1)求Q点的坐标；

(2)指出圆心T一定在哪一条直线上运动；

(3)当点H在直线上．且⊙T的半径等于圆心T到原点距离的倍时，你能确定的值吗?若能，请求出的值；若不能，请你说明理由。(第23题图供分析参考用，可能出现两种情况)

22．(本小题满分9分)

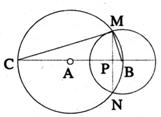
如图，BC是⊙A的直径，以B为圆心的圆与⊙A交于M、N两点，MN交BC于点P，

(1)说出CM与⊙B的位置关系，并简要说明理由；

(2)若⊙A的半径为2，⊙B的半径为1，求CM和MN的长。

21．(本小题满分8分)

田忌赛马是一个为人熟知的故事，传说战国时期，齐王与田忌各有上、中、下三匹马，同等级的马中，齐王的马比田忌的马强．有一天，齐王要与田忌赛马，双方约定：比赛三局，每局各出一匹，每匹马赛一次，赢得两局者为胜．看样子田忌似乎没有什么胜的希望，但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强……

(1)如果齐王将马按上中下的顺序出阵比赛。那么田忌的马如何出阵，田忌才能取胜?

(2)如果齐王将马按上中下的顺序出阵，而田忌的马随机出阵比赛，田忌获胜的概率是多少?(要求写出双方对阵的所有情况)

20．(本小题满分8分)

(1)解方程组：

(2)如图，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了?”心里很是纳闷。经过了解，教学楼、水塔的高分别为20m和30m，它们之间的距离为30m，小张身高为1.6m。小张要想看到水塔，他与教学楼的距离至少应有多少米?

19．(本小题满分7分)

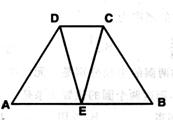
(1)已知：如图，梯形ABCD中，AB∥CD，AD=BC，E是底边AB的中点。

求证：DE=CE

(2)如图，在一次龙卷风中，一棵大树在离地面若干米处折断倒下，B为折断处最高点，树顶A落在离树根C的12米处，测得∠BAC=30°，求BC的长。(结果保留根号)。

18．(本小题满分7分)

(1) 已知两个分式：，，其中．下面有三个结论：

①A=B；　　 ②A、B互为倒数；　　 ③A、B互为相反数．通过计算得出正确结论．

(2) 解不等式组：

17．如图，△OAP、△ABQ均是等腰直角三角形，点P、Q在函数的图像上，直角顶点A、B均在轴上，则点B的坐标为__________________ 。(保留根号)

16．在很小的时候，我们就用手指练习过数数．一个小朋友按如图所示的规则练习数数，数到2006时对应的指头是__________________ (填出指头的名称，各指头的名称从上到下依次为大拇指、食指、中指、无名指、小指)．

15．如图，在Rt△ABC中，∠C=90°，AC=BC=，分别以A、B、C为圆心，以AC为半径画弧，三条弧与边AB所围成的阴影部分面积为__________________．(保留)

14．为了估计池塘里有多少条鱼，从池塘里捕捞了1000条鱼做上标记，然后放回池塘里，经过一段时间，等有标记的鱼完全混合于鱼群中以后，再捕捞200条，若其中有标记的鱼有10条，则估计池塘里有鱼__________________条．