24．如图，已知点A(1，0)，B(2，0)为直角坐标系内两点，点C在x轴负半轴上，且OC=2OA，以A为圆心，OA为半径作☉A，直线CD切OA于D点，连结OD．

(1)求点D的坐标；

(2)求图象经过0、B、D三点的二次函数的关系式

23．已知：如图AB∥CD，AD∥CE，且∠ACB=90º，E是AB的中点．

　 (1)试说明DE与AC互相垂直平分；

　 (2)探究l，当四边形AECD是正方形时，∠B的度数是多少?

(3)探究2，当四边形ABCD是等腰梯形时，∠B的度数是多少?

22．某家电集团公司生产某种型号的新家电，前期投资200万元，每生产一台这种新家电，后期还需要其它投资0．3万元，已知每台新家电可实现产值0．5万元。

(1)分别求总投资y₁(万元)和总利润y₂(万元)关于新家电的总产量z(台)的函数关系式，并画出函数y₂的图象；

　 (2)请你利用第(1)小题中的图象回答：当新家电的总产量为900台时，该公司是亏损还是盈利；

　 (3)请你利用第(1)小题中y₂与z的关系式，分析该公司的盈亏情况．

　 (注：总投资=前期投资+后期其它投资，总利润=总产值一总投资)

21．我市计划向贫困地区赠送一批电视机，首批270台将于近期启运．经与某运输公司联系，得知用A型汽车若干辆刚好装完；用B型汽车不仅可以少用l辆，而且有一辆车差30台电视机才装满．

　 (1)已知B型汽车比A型汽车每辆可多装15台，求A、B两种型号的汽车各能装电视机多少台?

　 (2)已知A型汽车的运费是每辆350元，B型汽车的运费是每辆400元，请你设计最节省运费的运输方案，并写出简要推理过程．

20．为了了解学校开展“孝敬父母，从家务事做起”活功的实施情况，该校抽取初二年级50名学生，调查他们一周(按七天计算)做家务所用时间(单位：小时)，得到一组数据，并绘制成下表，请根据该表完成下列各题：

分组	频数累计	频数	频率
O．55-1．05	正正	14	0．28
1．05-1．55	正正正	15	0．30
1．55-2．05	正	7	x
2．05-2．55		4	0．08
2．55-3．05	正	5	0．10
3．05-3．55		3	y
3．55-4．05		z	0．04
合计		50	1．00

(1)在以上频率分布表中，x=　　　 ，y=　　　 ，z=　　　　　

(2)这组数据中的中位数落在　　　　　 范围内；

(3)由以上信息判断，每周做家务的时间不超过1．5小时的学生所占百分比是　　　

　 (4)针对以上情况，写一个20字以内倡导“孝敬父母，热爱劳动”的句子　　　　　　

19．现在要把如图所示的一块等腰三角形(AB=AC)钢板切割后再焊接成一块矩形钢板，使矩形的面积正好等于该三角形的面积(切割的损失忽略不计)．

(1)请你设计两种不同的切割、焊接方案(每种方案切割的次数最多两次)，并用简要的文字和图形加以说明；

(2)若把该三角形钢板切割后焊接成正方形零件(只切割一次)，则该三角形需满足什么条件?)

18．如图，已知∠ACB=90°，AB=13，AC=12，∠BCM=∠BAC．

(1)求sin∠BAC的值；

　 (2)求点B到直线MC的距离．

17．如图，数轴上表示l、互的对应点分别为A、B，点B关于点A的对称点为C，设点C表示的数为x，求的值．

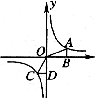
16．如图，A、C是函数图象上任意两点，过A作x轴的垂线AB，垂足为B，过C作y轴的垂线CD，D为垂足，记△AOB的面积为S₁，△COD的面积为是S₂，则S₁与S₂的大小关系是　　　　　　

15．掷两枚分别标有1，2，3，4，5，6，六个数字的正方体骰子，把两个骰子的点数相加，下列事件按发生的概率由小到大重新排列，(1)和为1；(2)和为6；(3)和为12；(4)和小于20，顺序应为