6．因式分解：=_________________________．

5．如果用□表示1个立方体，用表示两个立方体重叠，用表示三个立方体重叠，那么，如图1，是由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是(　　 )

4．用两块边长为a的等边三角形纸片拼成的四边形是(　　 )

A．等腰梯形　　 B．正方形　　 C．矩形　　 D．菱形

3．关于的一元二次方程的一个根是0，则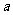的值为(　　 )

A．1　　 B．0 　　C．-1　　 D．±1

2．世界文化遗产长城的总长度约为670 000m，用科学记数法表示为(　　 )

A．　　 B．　　 C．　　 D．

1．下面是一名同学所做的5道练习题：①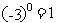；②；③；④；⑤；他做对的题数是(　　 )

A．0　　 B．1 　　C．2　　 D．3

26．(本小题满分8分)探索：在如图(1)至图(3)中，△ABC的面积为a．

(1)如图(1)，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S₁，则S₁=____________(用含a的代数式表示)；

(2)如图(2)，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S₂，则S₂=__________(用含a的代数式表示)，并写出理由；

(3)在图(2)的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF(如图3)．若阴影部分的面积为S₃，则S₃=__________(用含a的代数式表示)．

发现　 像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF(如图3)，此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的__________倍．

应用　 去年在面积为10m²的△ABC空地上栽种了某种花卉．今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH(如图4)．求这两次扩展的区域(即阴影部分)面积共为多少m²?

25．(本大题满分10分)

第三届南宁国际龙舟赛于2006年6月3日至4日在南湖举行，甲、乙两队在比赛时，路程(米)与时间(分钟)的函数图象如图所示，根据函数图象填空和解答问题：

(1)最先到达终点的是___________队，比另一队领先_____________分钟到达；

(2)在比赛过程中，乙队在_______分钟和________分钟时两次加速，图中点A的坐标是____________，点B的坐标是________________．

(3)假设乙队在第一次加速后，始终保持这个速度继续前进，那么甲、乙两队谁先到达终点？请说明理由．

24．(本小题满分8分)我市对城区沿小康河两岸的部分路段进行亮化工程建设，整个工程拟由甲、乙两个安装公司共同完成．从两个公司的业务资料看到：若两个公司合做，则恰好用12天完成；若甲、乙合做9天后，由甲再单独做5天也恰好完成．如果每天需要支付甲、乙两公司的工程费用分别为1.2万元和0.7万元．

试问：(1)甲、乙两公司单独完成这项工程各需多少天?

(2)要使整个工程费用不超过22.5万元，则乙公司最少应施工多少天?