24．如图，直角梯形ABCD中，AD//BC，∠B=90°，AB=12cm，BC=9cm，DC=13cm，点P是线段AB上一个动点。设BP为xcm，△PCD的面积为。

(1)求AD的长；

(2)求y与x之间的函数关系式，并求出当x为何值时，y有最大值？最大值是多少？

(3)在线段AB上是否存在点P，使得△PCD是直角三角形？若存在，求出x的值；若不存在，请说明理由。

23．如图1，点P是线段MN的中点，请你利用该图形画一对以点P为对称中心的全等三角形。

请你参考这个作全等三角形的方法，解答下列问题：

图1

(1)如图2，在Rt△ABC中，∠BAC=90°，AB>AC，点D是BC边中点，过D作射线交AB于E，交CA延长线于F，请猜想∠F等于多少度时，BE=CF(直接写出结果，不必证明)。

图2

(2)如图3，在△ABC中，如果∠BAC不是直角，而(1)中的其他条件不变，若BE=CF的结论仍然成立，请写出△AEF必须满足的条件，并加以证明。

图4

22．如图，在⊙O中，弦AB与半径相等，连结OB并延长，使BC=OB。

(1)试判断直线AC与⊙O的位置关系，并证明你的结论；

(2)请你在⊙O上找到一个点D，使AD=AC(完成作图，证明你的结论)，并求∠ABD的度数。

21．某高速公路检测点抽测了200辆汽车的车速，并将检测结果绘制出部分车速频率分布直方图(每组包含最大值不包含最小值)，如图所示。根据以上信息，解答下列问题：

(1)补全频率分布直方图；

(2)按规定，车速在70千米/时-120千米/时范围内为正常行驶，试计算正常行驶的车辆所占的百分比；

(3)按规定，车速在120千米/时以上时为超速行驶，如果该路段每天的平均车流量约为1万辆，试估计每天超速行驶的车辆数。

20．在平面直角坐标系xOy中，一次函数的图象与反比例函数的图象交于点，与y轴交于点B。

(1)求这个一次函数的解析式；

(2)求△AOB的面积。

19．某社区在举办“文明奥运”宣传活动时，使用了如图所示的一种简易活动桌子(桌面AB与地面平行)。现测得OA=OB=30cm，OC=OD=50cm，若要求桌面离地面的高度为40cm，求两条桌腿的张角∠COD的度数。

18．如图，在正方形ABCD中，点E、F分别在BC、CD上，BE=CF，连结AE、BF相交于点G。现给出了四个结论：①AE=BF；②∠BAE=∠CBF；③BF⊥AE；④AG=FG。请在这些结论中，选择一个你认为正确的结论，并加以证明。

结论：_____________________________________________。

证明：

17．解不等式组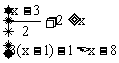，并把其解集在数轴上表示出来。

16．解分式方程

15．先化简，再求值：，其中