23．(本题满分l2分)

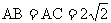在△ABC中，∠BAC=90°，，圆A的半径为1，如图所示，若点O在BC边上运动(与点B、C不重合)，设，△AOC的面积为，

(1)求关于的函数解析式，并写出函数的取值范围。

(2)以点O为圆心，BO长为半径作圆O，求当圆O与圆A相切时，△AOC的面积。

22．(本题满分l2分)

如图，在△ABC中，∠BAC=90°延长BA到点D，使，点E、F分别为BC、AC的中点，

(1)求证：DF=BE

(2)过点A作AG∥BC，交DF于点G，求证AG=DG。

21．(本小题10分)青少年视力水平的下降已经引起全社会的关注，某校为了了解初中毕业年级500名学生的视力情况，从中抽查了一部分学生视力，通过数据处理，得到如下频率分布表和频率分布直方图：

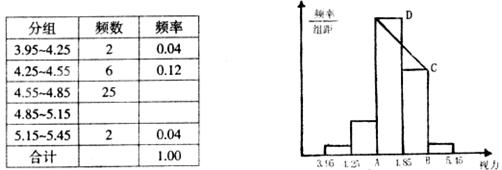
请你根据给出的图表回答：

(1)填写频率分布表中未完成部分的数据：

(2)在这个问题中，总体是　　　　　　　　 ，样本容量是　　　　　　　　　　　 。

(3)在频率分布直方图中梯形ABCD的面积是　　　　　　　　　　　　　　 。

(4)请你用样本估计总体，可以得到哪些信息(写一条即可)　　　　　　　　　　　 。

20．(本题满分l0分)

甲、乙两超市同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满l00元，均可得到一次摸奖的机会，在一个纸盒里装有2个红球和2个白球，除颜色外，其它全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少(如下表)。

甲超市

乙超市

如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由。

19．(本题满分8分)先化简，再求值

，其中

18．如图，在直线m上摆着三个正三角形：△ABC、△HFG、△DCE，已知，F、G分别是BC、CE的中点，FM∥AC、GN∥DC。设图中三个平行四边形的面积依次是S₁、S₂、S₃，若S₁+S₃=10则S₂=　　　　　 。

17．有一圆柱体高为10cm，底面圆的半径为4cm，AA₁、BB₁为相对的两条母线。在AA₁上有一个蜘蛛Q，QA=3cm；在BB₁上有一只苍蝇P，PB₁=2cm。蜘蛛沿圆柱体侧面爬到P点吃苍蝇，最短的路径是　　　　 cm。(结果用带和根号的式子表示)

16．关于不等式组只有4个整数解，则的取值范围是　　　　　　 。

15．二次函数的图像如图所示，则的值是　　　　 。

14．将矩形ABCD置于直角坐标系中，使点A与坐标的原点重合，边AB、AD分别落在轴、轴上(如图①)，再将此矩形在坐标系平面内按逆时针方向绕原点旋转30°(如图②)，若AB=4，BC=3，则图②中的点B的坐标为　　　　　　　 ；点C的坐标为　　　　 　。