1 9．(本题满分6分)

　　 有一道题：“先化简，再求值：，其中“x=一”．小亮同学做题时把“x= 一”错抄成了“z=”，但他的计算结果也是正确的，请你解释这是怎么,回事．

2 0．(本题满分8分)

　　 一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同)，其中红球有2个，黄球有1个，从中任意捧出1球是红球的概率为．

　 (1)试求袋中绿球的个数；

　　 (2)第1次从袋中任意摸出l球(不放回)，第2次再任意摸出1球，请你用画树

状图或列表格的方法，求两次都摸到红球的概率．

2 1．(本题满分8分)

如图，某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点有人求救，便立即派三名救生员前去营救．1号救生员从A点直接跳入海中；2号救生员沿岸边(岸边看成是直线)向前跑到C点，再跳入海中；3号救生员沿岸边向前跑3 0 O米到离B点最近的D点，再跳人海中．救生员在岸上跑的速度都是6米／秒，在水中游泳的速度都是2米／秒．若∠BAD=4 5°，∠BCD=6 0°，三名救生员同时从A点出发，请说明谁先到达营救地点B．　 (参考数据≈1.4，≈1.7)

2 2．(本题满分9分)

数学老师将本班学生的身高数据(精确到l厘米)交给甲、乙两同学，要求他们各自独立地绘制一幅频数分布直方图．甲绘制的如图①所示，乙绘制的如图②所示，经确认，甲绘制的图是正确的，乙在整理数据与绘图过程中均有个别错误．

请回答下列问题：

　　 (1)该班学生有多少人?

　 　(2)甲同学身高为1 6 5厘米，他说：“我们班上比我高的人不超过1/4”．他的说法正确吗?说明理由．

　　 (3)写出乙同学在整理或绘图过程中的错误(写出一个即可)．

　　 (4)设该班学生的身高数据的中位数为a，试写出a的值

2 3．(本题满分9分)

生活中，有人喜欢把传送的便条折成形状　　　 ，折叠过程是这样的(阴影部分表示纸条的反面)：

　　 如果由信纸折成的长方形纸条(图①)长为2 6 cm，宽为xcm，分别回答下列问题：

　　 (1)为了保证能折成图④的形状(即纸条两端均超出点P)，试求x的取值范围．

(2)如果不但要折成图④的形状，而且为了美观，希望纸条两端超出点P的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点M与点A的距离(用x表示)．

2 4．(本题满分1 0分)

　　 某工厂生产的某种产品按质量分为1 0个档次．第1档次(最低档次)的产品一天能生产7 6件，每件利润10元．每提高一个档次，每件利润增加2元，但一天产量减少4件．

　　 (1)若生产第x档次的产品一天的总利润为y元(其中x为正整数，且1≤x≤10)，求出y关于x的函数关系式；

(2)若生产第x档次的产品一天的总利润为1080元，求该产品的质量档次．

2 5．(本题满分1 4分)

　　 如图，等腰梯形ABCD中，AD∥BC，点E是线段AD上的一个动点(E与A、D不重合)，G、F、H分别是BE、BC、CE的中点．

　　 (1)试探索四边形EGFH的形状，并说明理由．

　　 (2)当点E运动到什么位置时，四边形EGFH是菱形?并加以证明．

(3)若(2)中的菱形EGFH是正方形，请探索线段EF与线段BC的关系，并证明你的结论．

2 6．(本题满分1 4分)

如图，在平面直角坐标系中，坐标原点为O，A点坐标为(4，0)，B点坐标为(一1，0)，以AB的中点P为圆心，AB为直径作⊙ P与y轴的正半轴交于点C．

(1)求经过A、B、C三点的抛物线对应的函数表达式．

　　 (2)设M为(1)中抛物线的顶点，求直线MC对应的函数表达式．

(3)试说明直线MC与⊙ P的位置关系，并证明你的结论．

　　　　　　　　　　　　　　　 　　　　　　　　　　　(第26题图)

18．观察下列各式：

请你将发现的规律用含自然数n(n≥1)的等式表示出来　　　　　　　　　　　　　 ．

17．在计算器上，按照下面的程序进行操作：　

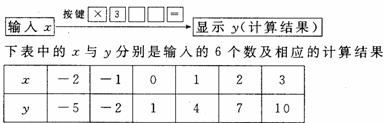
上面操作程序中所按的第三个键和第四个键应是□□．

16．如图，电影胶片上每一个图片的规格为3．5 cm×3．5 cm，放映屏幕的规格为

2 m×2 m，若放映机的光源S距胶片2 0 cm，那么光源S距屏幕　　　　 ，米时，放映的

图象刚好布满整个屏幕．

15．如图，在数轴上点A和点B之间表示整数的点有　　　　 个．

14．请你写一个能先提公因式、再运用公式来分解因式的三项式，并写出分解因式的结果　　　　　　　　　　　　　　　 ．

13．股市有风险，投资须谨慎．截止今年5月底，我国股市开户总数约95000000，正向1亿挺进，95000000用科学记数法表示为　　　　 ．

12．下列图形中阴影部分的面积相等的是

A．①②　　 B．②③　　　 C．③④　　 D．①④

第 Ⅱ 卷

11．小明、小亮、小梅、小花四人共同探究代数式x²一4x+5的值的情况．他们作了如下分工：小明负责找值为1时x的值，小亮负责找值为0时x的值，小梅负责找最小值，小花负责找最大值．几分钟后，各自通报探究的结论，其中错误的是

　　 A．小明认为只有当x=2时，x²一4x+5的值为1

　　 B．小亮认为找不到实数x，使x²一4x+5的值为O

　　 C．小梅发现x²一4x+5的值随x的变化而变化，因此认为没有最小值

　　 D．小花发现当x取大于2的实数时，x²一4x+5的值随x的增大而增大，因此认为没有最大值.

10．将n个边长都为lcm的正方形按如图所示的方法摆放，点A₁，A₂，……，A_n分别是正方形的中心，则n个这样的正方形重叠部分(阴影部分)的面积和为

A．cm。　　 　　　B．cm²

C．cm²　 　　　 D．cm²