5. 某鞋店试销一种新款运动鞋,试销期间销售情况如下表:

　 对于这个鞋店的经理来说最关心的是哪种型号的鞋畅销,则下列统计量对鞋店经理来说最有意义的是

A. 平均数 B. 众数 C. 中位数　　　　　 D. 标准差

4. 如图,是一个物体的三视图,则该物体的形状是

A. 圆锥 　B.圆柱　　　　　　　 C. 三棱锥 　　　D. 三棱柱

3. 在函数中,自变量x的取值范围是

A. 　　　B. 　　　　　C. 　　　　　　D.

2. 废电池是一种危害严重的污染源，一粒纽扣电池可以污染600 000升水,用科学记数法表示这个数为

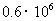A. 升 B. 升　　　　 C. 升D. 升

1. -5的绝对值是

　 A. 　　　　　　B. -　　　　　　 C. 5　　　　　　　　 D. -5

24．△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，把一个三角板的直角顶点放在点D处，将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .

(1)如图1，观察旋转过程，猜想线段AF与BE的数量关系并证明你的结论；

(2)如图2，若连接EF，请探索线段BE、EF、FC之间的关系；

(3)如图3，若将“AB=AC，点D是BC的中点”改为：“∠B=30°，AD⊥BC于点D”，其余条件不变，探索(1)中结论是否成立？若不成立，请探索关于AF、BE的比值.

解：

23. 抛物线交x轴于A、B两点，交y轴于点C，已知抛物线的对称轴为直线x = -1，B(1,0)，C(0,-3).

　 (1)求抛物线的解析式；

　 (2)在抛物线对称轴上是否存在一点P，使点P到A、C两点

距离之差最大？若存在，求出点P坐标；若不存在，请说明理由.

解：(1)

(2)

22．如图，梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=，在线段BC上取一点P，连结DP，作射线PE⊥DP，PE与直线AB交于点E.

(1)试确定CP=3时，点E的位置；

(2)若设CP=x，BE=y，试写出y关于自变量x的

函数关系式；

(3)若在线段BC上只找到唯一一点P，使上述作法得到的点E与点A重合，试求出此时的值.

解：

21．五一期间，某区一中、二中组织100名优秀教师去某景区旅游，(其中一中教师多于二中教师)，景区门票价格规定如下表：

若两校都以校为单位一次性购票，则两校一共需付4725元，求两校各有多少名优秀教师参加这次旅游？若两校联合起来，作为一个团体购票，能节约多少钱？

20．将网格中的图形以点O为位似中心放大为原来的2倍，画出一个放大后的图形即可.

　解：