6．如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC相似的是(　　 )

5．关于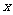的一元二次方程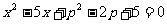的一个根为1，则实数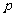的值是(　 　)

A．4　　　　　　　　　　　　　　 B．0或2 　　　　　　　　 C．1　　 　　　　　　　　　　 D．－l

4．如果梯形的上底长为4，中位线长为5，那么此梯形的下底长为(　　 )

A．6　　　　　　　　　　　　　　 B．5 　　　　　　　　　　　　 C．4　　 　　　　　　　　　　 D．3

3．如下图，在平面直角坐标系中，A点坐标为(3, 4)，将OA绕原点O逆时针旋转90°得到OA’，则点A’的坐标是(　　 )

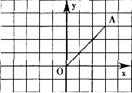
A．(－4, 3)　　 　　　　 B．(－3, 4)　 　　　　　　 C．(3, －4)　　 　　　　　　　 D．(4, －3)

2．代数式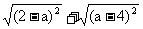的值是常数2，则a的取值范围是( 　　)

A．a≥4　　　　　　　　　　　 B．a≤2 　　　　　　　　　 C．2≤a≤4 　　　　　　　　 D．a=2或a=4

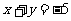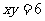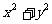1．已知，，则的值是(　　 )

A．1　　　　　　　　　　　　　　 B．13 　　　　　　　　　　　 C．17　　 　　　　　　　　　 D．25

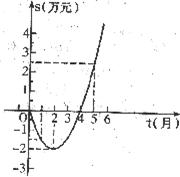
25．(12分)为了顺应市场要求，我市某花炮厂技术部研制开发一种新产品，年初上市后，公司经历了从亏损到盈利的过程，下面的二次函数图像(部分)刻画了该厂年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系)根据图象提供的信息，解答下列问题：　　

(1)由已知图象上的三点坐标，求累积利润s(万元)与时间t(月)之间的函数关系式；　

(2)求截止到几月末花炮厂累积利润可达到30万元?　　

(3)求第8个月公司所获利润是多少万元?

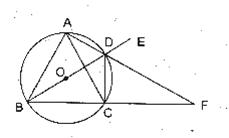
24．(10分)如图，⊙O为△ABC的外接圆，且AB=AC，过点A的直线交⊙O于D，交BC延长线于F，DE是BD的延长线，连结CD．　　　

(1)求证：EDF=CDF；

(2)求证：；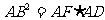　　　

(3)若BD正好是⊙O的直径，且EDC=120°，BC=6cm，求AF的长．

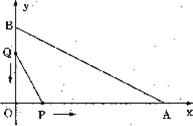
23．(10分)如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米。点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t(秒)表示移动的时间(0≤t≤6)，那么

(1)设△POQ的面积为y，求y关于t的函数解析式；　　

(2)当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；　　

(3)当t为何值时，△POQ与△AOB相似．　　

22．(8分)任意剪一个三角形纸片，如图中的△ABC，不妨设它的一个锐角为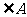，首先利用对折的方法得到高AN。然后按图中所示的方法分别将含有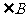、的部分向里折，找出AB、AC的中点D、E，同时得到两条折痕DF、EG，分别沿折痕DF、EG剪下图中的三角形①，②，并按图中箭头所指的方向分别旋转180°。

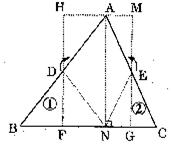
(1)你能拼成一个什么样的四边形?并说明你的理由；　　　

(2)请你利用这个图形，证明三角形的面积公式：S=底高。