
28.(本小题满分10分)
如图,平面上一点 从点
从点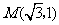 出发,沿射线
出发,沿射线 方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以
方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以 为对角线的矩形
为对角线的矩形 的边长
的边长 ;过点
;过点 且垂直于射线
且垂直于射线 的直线
的直线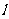 与点
与点 同时出发,且与点
同时出发,且与点 沿相同的方向、以相同的速度运动.
沿相同的方向、以相同的速度运动.
(1)在点 运动过程中,试判断
运动过程中,试判断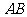 与
与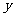 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
(2)设点 与直线
与直线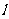 都运动了
都运动了 秒,求此时的矩形
秒,求此时的矩形 与直线
与直线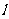 在运动过程中所扫过的区域的重叠部分的面积
在运动过程中所扫过的区域的重叠部分的面积 (用含
(用含 的代数式表示).
的代数式表示).

27.(本小题满分8分)
王大伯要做一张如图1的梯子,梯子共有8级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度 ,最下面一级踏板的长度
,最下面一级踏板的长度
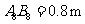 .木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
.木工师傅在制作这些踏板时,截取的木板要比踏板长,以保证在每级踏板的两个外端各做出一个长为4cm的榫头(如图2所示),以此来固定踏板.现市场上有长度为2.1m的木板可以用来制作梯子的踏板(木板的宽厚和厚度正好符合要制作梯子踏板的要求),请问:制作这些踏板,王大伯最少需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)

26.(本小题满分9分)
小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后 分钟时,他所在的位置与家的距离为
分钟时,他所在的位置与家的距离为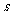 千米,且
千米,且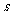 与
与 之间的函数关系的图像如图中的折线段
之间的函数关系的图像如图中的折线段 所示.
所示.
(1)试求折线段 所对应的函数关系式;
所对应的函数关系式;
(2)请解释图中线段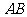 的实际意义;
的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离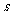 (千米)与小明出发后的时间
(千米)与小明出发后的时间 (分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)

25.(本小题满分6分)
图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了 层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为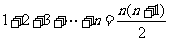 .
.
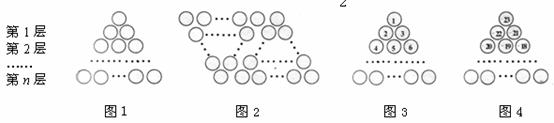
如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数

 ,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数
,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数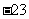 ,
,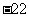 ,
, ,
, ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.
24.(本小题满分6分)
某商场搞摸奖促销活动:商场在一只不透明的箱子里放了三个相同的小球,球上分别写有“10元”、“20元”、“30元”的字样.规定:顾客在本商场同一日内,每消费满100元,就可以在这只箱子里摸出一个小球(顾客每次摸出小球看过后仍然放回箱内搅匀),商场根据顾客摸出小球上所标金额就送上一份相应的奖品.现有一顾客在该商场一次性消费了235元,按规定,该顾客可以摸奖两次,求该顾客两次摸奖所获奖品的价格之和超过40元的概率.
23.(本小题满分8分)
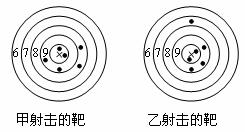
如图是甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数)每人射击了6次.
(1)请用列表法将他俩的射击成绩统计出来;
(2)请你用学过的统计知识,对他俩的这次射击情况进行比较.
22.(本小题满分6分)
如图,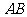 是⊙
是⊙ 的直径,
的直径, 切⊙
切⊙ 于
于 ,
, 交⊙
交⊙ 于
于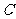 ,连
,连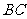 .若
.若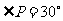 ,求
,求 的度数.
的度数.

21.(本小题满分7分)
如图,已知四边形 是菱形,点
是菱形,点 分别是边
分别是边 ,
, 的中点.求证:
的中点.求证: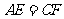 .
.

20.(本题共2小题,第(1)小题4分,第(2)小题6分,满分10分)
(1)计算: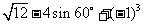 ;
;
(2)解不等式组 并写出它的所有整数解.
并写出它的所有整数解.
19.任何一个正整数 都可以进行这样的分解:
都可以进行这样的分解: (
(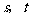 是正整数,且
是正整数,且 ),如果
),如果 在
在 的所有这种分解中两因数之差的绝对值最小,我们就称
的所有这种分解中两因数之差的绝对值最小,我们就称 是
是 的最佳分解,并规定:
的最佳分解,并规定: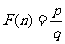 .例如18可以分解成
.例如18可以分解成 ,
, ,
,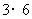 这三种,这时就有
这三种,这时就有 .给出下列关于
.给出下列关于 的说法:(1)
的说法:(1) ;(2)
;(2) ;(3)
;(3)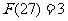 ;(4)若
;(4)若 是一个完全平方数,则
是一个完全平方数,则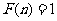 .其中正确说法的个数是( )
.其中正确说法的个数是( )
A. B.
B.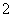 C.
C.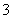 D.
D.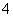
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com