
3.下列计算中,正确的是( )
(A)a3·a4=a12 (B) (a2)3=a5 (C)a6÷a2=a3 (D) (-ab)3=-a3b3
2.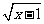 实数范围内有意义,则x的取值范围是( )
实数范围内有意义,则x的取值范围是( )
(A)x>1 (B)x≥l (C)x<1 (D)x≤1
1.- 的绝对值等于(
)
的绝对值等于(
)
(A)-2 (B)2 (C) - (D)
(D) 
28.(本题10分)
如图,梯形 在平面直角坐标系中,上底
在平面直角坐标系中,上底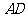 平行于
平行于 轴,下底
轴,下底 交
交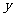 轴于点
轴于点 ,点
,点 (4,
(4, ),点
),点 ,
, ,
, .
.
(1)求直线 的解析式;
的解析式;
(2)若点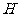 的坐标为
的坐标为 ,动点
,动点 从
从 出发,以1个单位/秒的速度沿着
出发,以1个单位/秒的速度沿着 边向
边向 点运动(点
点运动(点 可以与点
可以与点 或点
或点 重合),求
重合),求 的面积
的面积 (
( )随动点
)随动点 的运动时间
的运动时间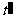 秒变化的函数关系式(写出自变量
秒变化的函数关系式(写出自变量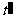 的取值范围);
的取值范围);
(3)在(2)的条件下,当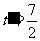 秒时,点
秒时,点 停止运动,此时直线
停止运动,此时直线 与
与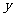 轴交于点
轴交于点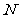 .另一动点
.另一动点 开始从
开始从 出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由
出发,以1个单位/秒的速度沿着梯形的各边运动一周,即由 到
到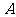 ,然后由
,然后由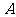 到
到 ,再由
,再由 到
到 ,最后由
,最后由 回到
回到 (点
(点 可以与梯形的各顶点重合).设动点
可以与梯形的各顶点重合).设动点 的运动时间为
的运动时间为 秒,点
秒,点 为直线
为直线 上任意一点(点
上任意一点(点 不与点
不与点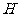 重合),在点
重合),在点 的整个运动过程中,求出所有能使
的整个运动过程中,求出所有能使 与
与 相等的
相等的 的值.
的值.
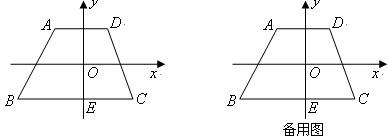
27.(本题10分)
如图1,在正方形 中,对角线
中,对角线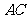 与
与 相交于点
相交于点 ,
, 平分
平分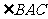 ,交
,交 于点
于点 .
.
(1)求证: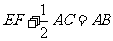 ;
;
(2)点 从点
从点 出发,沿着线段
出发,沿着线段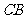 向点
向点 运动(不与点
运动(不与点 重合),同时点
重合),同时点 从点
从点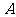 出发,沿着
出发,沿着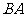 的延长线运动,点
的延长线运动,点 与
与 的运动速度相同,当动点
的运动速度相同,当动点 停止运动时,另一动点
停止运动时,另一动点 也随之停止运动.如图2,
也随之停止运动.如图2, 平分
平分 ,交
,交 于点
于点 ,过点
,过点 作
作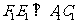 ,垂足为
,垂足为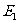 ,请猜想
,请猜想 ,
,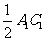 与
与 三者之间的数量关系,并证明你的猜想;
三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当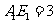 ,
,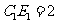 时,求
时,求 的长.
的长.

26.(本题8分)
青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价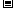 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过400元 |
售价打九折 |
|
超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
25.(本题8分)
据2007年5月26日《生活报》报道,我省有关部门要求各中小学要把“每天锻炼一小时”写入课表.为了响应这一号召,某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图.请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?

24.(本题6分)
现将三张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3).
分别在图1、图2、图3中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,并把这两部分重新拼成符合下列要求的几何图形.
要求:
(1)在左边的平行四边形纸片中画一条裁剪线,然后在右边相对应的方格纸中,按实际大小画出所拼成的符合要求的几何图形;
(2)裁成的两部分在拼成几何图形时要互不重叠且不留空隙;
(3)所画出的几何图形的各顶点必须与小正方形的顶点重合.

23.(本题6分)
如图, 是
是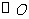 的弦,矩形
的弦,矩形 的边
的边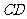 与
与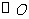 交于点
交于点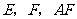 和
和 相交于点
相交于点 ,连接
,连接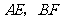 .
.

(1)写出图中每一对全等的三角形(不再添加辅助线);
(2)选择你在(1)中写出的全等三角形中的任意一对进行证明.
22.(本题6分)
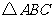 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)作出与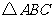 关于
关于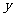 轴对称的
轴对称的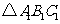 ;
;
(2)将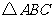 向下平移3个单位长度,画出平移后的
向下平移3个单位长度,画出平移后的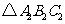 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com