
9.如图, 是圆O上三点,
是圆O上三点,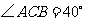 ,则
,则 等于 度.
等于 度.
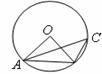
8.方程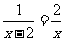 的解为
的解为 .
.
7.分解因式: .
.
6.比较大小:
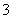 (填“
(填“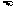 ,
,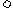 或
或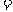 ”符号)
”符号)
5.平面直角坐标系中有六个点 ,
,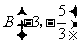 ,
, ,
, ,
, ,
, ,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是
,其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是
A.点 B.点
B.点 C.点
C.点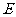 D.点
D.点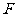
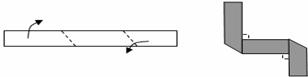
4.如左图所示,将长为20cm,宽为2cm的长方形白纸条,折成右图所示的图形并在其一面着色,则着色部分的面积为( )
A. B.
B.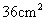 C.
C.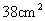 D.
D.
3.小明五次跳远的成绩(单位:米)是:3.6,3.8,4.2,4.0,3.9,这组数据的中位数是( )
A.3.9米 B.3.8米 C.4.2米 D.4.0米
2.据2006年末的统计数据显示,免除农村义务教育阶段学杂费的西部地区和部分中部地区的学生约有52000000名,这个学生人数用科学记数法表示正确的是( )
A.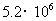 B.
B.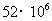 C.
C.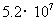 D.
D.
1. 的倒数是( )
的倒数是( )
A.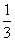 B.
B. C.
C.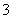 D.
D.
17.(本题6分)解方程:x2-x-1=0。
18.(本题6分)化简求值: ,其中x=2。
,其中x=2。
19.(本题6分)你一定玩过跷跷板吧!如图是小明和小刚玩跷跷板的示意图,横板绕它的中点O上下转动,立柱OC与地面垂直。当一方着地时,另一方上升到最高点。问:在上下转动横板的过程中,两人上升的最大高度AA’、BB’有何数量关系?为什么?

20.(本题7分)如图①是一个美丽的风车图案,你知道它是怎样画出来的吗?按下列步骤可画出这个风车图案:在图②中,先画线段OA,将线段OA平移至CB处,得到风车的第一个叶片F1,然后将第一个叶片OABC绕点O逆时针旋转180°得到第二个叶片F2,再将F1、F2同时绕点O逆时针旋转90°得到第三、第四个叶片F3、F4。根据以上过程,解答下列问题:
(1)若点A的坐标为(4,0),点C的坐标为(2,1),写出此时点B的坐标;
(2)请你在图②中画出第二个叶片F2;
(3)在(1)的条件下,连接OB,由第一个叶片逆时针旋转180°得到第二个叶片的过程中,线段OB扫过的图形面积是多少?

21.(本题7分)某区七年级有3000名学生参加“安全伴我行知识竞赛”活动。为了了解本次知识竞赛的成绩分布情况,从中抽取了200名学生的得分(得分取正整数,满分为100分)进行统计。
|
分组 |
频数 |
频率 |
|
49.5-59.5 |
10 |
|
|
59.5-69.5 |
16 |
0.08 |
|
69.5-79.5 |
|
0.20 |
|
79.5-89.5 |
62 |
|
|
89.5-100.5 |
72 |
0.36 |
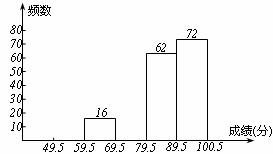
请你根据不完整的频率分布表,解答下列问题:
(1)补全频数分布直方图;
(2)若将得分转化为等级,规定得分低于59.5分评为“D”,59.5-69.5分评为“C”,69.5-89.5分评为“B”,89.5-100.5分评为“A”。这次全区七年级参加竞赛的学生约有多少学生参赛成绩被评为“D”?如果随机抽查一名参赛学生的成绩等级,则这名学生的成绩被评为“A”、“B”、“C”、“D”哪一个等级的可能性大?请说明理由。
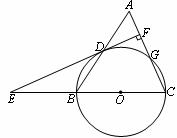
22.(本题8分)如图,等腰三角形ABC中,AC=BC=10,AB=12。以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E。
(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值。
23.(本题10分)康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台。从A、B两地运往甲、乙两地的费用如下表:
|
|
甲地(元/台) |
乙地(元/台) |
|
A地 |
600 |
500 |
|
B地 |
400 |
800 |
(1)如果从A地运往甲地x台,求完成以上调运所需总费用y(元)与x(台)的函数关系式;
(2)若康乐公司请你设计一种最佳调运方案,使总的费用最少,该公司完成以上调运方案至少需要多少费用?为什么?
24.(本题10分)填空或解答:点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
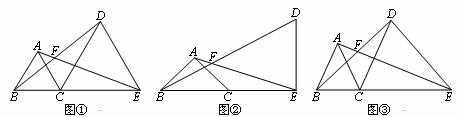

(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。
25.(本题12分)如图①,在平面直角坐标系中,Rt△AOB≌Rt△CDA,且A(-1,0)、B(0,2),抛物线y=ax2+ax-2经过点C。

(1)求抛物线的解析式;
(2)在抛物线(对称轴的右侧)上是否存在两点P、Q,使四边形ABPQ是正方形?若存在,求点P、Q的坐标,若不存在,请说明理由;
(3)如图②,E为BC延长线上一动点,过A、B、E三点作⊙O’,连结AE,在⊙O’上另有一点F,且AF=AE,AF交BC于点G,连结BF。下列结论:①BE+BF的值不变;②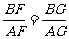 ,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。
,其中有且只有一个成立,请你判断哪一个结论成立,并证明成立的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com