
24.已知点E、F为抛物线 上的两点,过点E、F分别作
上的两点,过点E、F分别作 轴的垂线,分别交
轴的垂线,分别交 轴于点B、D,交直线
轴于点B、D,交直线 于点A、C,设S为直线AB、CD与
于点A、C,设S为直线AB、CD与 轴、直线
轴、直线 所围成图形的面积。
所围成图形的面积。
(1)当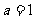 ,
, ,
, 时,计算:①当
时,计算:①当 ,
, 时,求
时,求 、
、 、S;②当
、S;②当 ,
,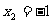 时,求
时,求 、
、 、S;通过以上的计算,猜想S与
、S;通过以上的计算,猜想S与 -
- 的数量关系;
的数量关系;
(2)当抛物线 在
在 轴上方,且点
轴上方,且点 、
、 在抛物线
在抛物线 的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
(3)如果将(2)中的“同侧”改为“异侧”(如图2),其他条件不变,并设M为直线 与
与 轴交点,
轴交点,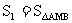 ,
,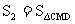 ,求
,求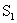 、
、 与
与 、
、 的数量关系(直接写出答案)。
的数量关系(直接写出答案)。

23.图1、图2、图3是分别由两个具有公共顶点A的正三角形、正四边形和正五边形组成的图形,且其中一个正多边形的顶点 在另一个正多边形的边BC上。
在另一个正多边形的边BC上。
(1)图1中, =
。(直接写出答案);
=
。(直接写出答案);
(2)图2中,求 ;
;
(3)图3中, =
。(直接写出答案);
=
。(直接写出答案);
(4)当满足条件的图形为正n边形时(如图4),猜想: = 。(直接写出答案)
= 。(直接写出答案)

22.节日里,姐妹两人在50米的跑道上进行短跑比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为am/s、bm/s。
(1)如果两人重新开始比赛,姐姐从起点向后退3 m,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的同时;若不能,请说明谁先到达终点;
(2)如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案。
21.如图,某探险队的8名队员在距营地210 km的地方遇险,营地负责人接到通知后,告知探险队全体人员步行返回营地,并派出一辆越野车以80 km/h的速度前去营救,2.5 h后越野车遇到探险队员,将其中4名队员送回营地,并立即返回接送其他队员,求越野车第二次接到队员时与营地的距离(越野车与探险队员的步行速度均近似为匀速,队员上、下车的时间忽略不计)。

20.现有若干个完全相同的硬币(硬币的正、反面图案不同),按如下方式抛掷硬币。
方式一:从中选取一枚硬币抛掷;
方式二:从中选取两枚硬币抛掷;
方式三:从中选取三枚硬币抛掷。
请你在每一种抛掷方式中,各找出一种随机现象,使得这三种随机现象的概率相等(要求:概率不能为0或1),并说明理由。
19.如图,在直角坐标系中,⊙A的圆心坐标为(1,-2),半径为1。
(1)圆心A与坐标原点O之间的距离为 ;
(2)画出⊙A关于 轴对称的图形;
轴对称的图形;
(3)当⊙A向上平移的距离d满足 条件时,⊙A 与它关于 轴对称的图形相切。
轴对称的图形相切。
18.某餐厅为了给假期来图书馆学习的学生提供营养早餐,特意派两个调查小组分别对假期在图书馆学习的学生的起床时问和吃早餐情况进行抽样调查,并分别把调查结果绘制成直方图(如图1)和扇形统计图(如图2)。

(1)被调查的学生共有 人,其中6:00-6:10起床的学生占被调查学生的 %(精确到1%);
(2)将扇形统计图补充完整;
(3)据统计,假期每天早晨到图书馆学习的学生约有320人,请你估计不能在家里吃营养早餐的学生数。
17.如图,在梯形ABCD中,AD∥BC,AB=DC,点O为底边AD的中点,求证:OB=OC。(要求:写出证明过程中的重要依据)

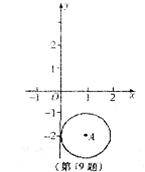
16.已知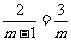 ,求关于
,求关于 的方程
的方程 的解。
的解。
15.如图,矩形OABC的两边OA、OC分别在 轴、
轴、 轴的正半轴上,OA=4,OC=2,点G为矩形对角线的交点,经过点G的双曲线
轴的正半轴上,OA=4,OC=2,点G为矩形对角线的交点,经过点G的双曲线 在第一象限的图象与BC相交于点M,则CM∶MB= 。
在第一象限的图象与BC相交于点M,则CM∶MB= 。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com