
7、如图所示,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC,分别取 ,
,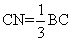 ,量得MN=38m,则AB的长是 ( )
,量得MN=38m,则AB的长是 ( )
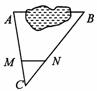
A、152m B、114m C、76m D、104m
6、如图所示,点O是等边三角形PQR的中心,P',Q', R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的位似比、位似中心分别是 ( )

A、2,点P B、 ,点P C、2,点O D、
,点P C、2,点O D、 ,点O
,点O
5、如图所示,P是Rt△ABC的斜边BC上异于B,C的一点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有 ( )

A、1条 B、2条 C、3条 D、4条
4、如图所示,在正方形的网格上,若使△ABC∽△PBD,则点P应在 ( )

A、P1处 B、P2处 C、P3处 D、P4处
3、在比例尺为1:20000的地图上,量得甲、乙两地的距离为5cm,则甲、乙两地的实际距离是 ( )
A、1km B、10km C、100km D、0.1km
2、计算 的正确结果是 ( )
的正确结果是 ( )
A、 B、0 C、
B、0 C、 D、
D、
1、函数 中,自变量x的取值范围是 ( )
中,自变量x的取值范围是 ( )
A、 B、
B、 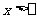 C、
C、 D、
D、
26.如图,菱形ABCD的边长为6 cm,∠DAB=60°,点M是边AD上一点,且DM= 2 cm,点E、F分别从A,C同时出发,以1 cm/s的速度分别沿边 AB、CB向点B运动,EM、CD的延长线相交于G,GF交AD于O.设运动时间为x(s),△CGF的面积为y( )
)
(1)求y与x之间的函数关系式;
(2)当x为何值时,GF⊥AD?
(3)是否存在某一时刻,使得线段GF把菱形ABCD分成的上、下两部分的面积之比为3∶7?若存在,求出此时x的值;若不存在,说明理由.
(参考数据: =1 681,
=1 681, =2 401,
=2 401, =2 601,
=2 601, =3 481.)
=3 481.)

25.第一象限内的点A在一反比例函数的图象上,过A作AB⊥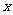 轴,垂足为B,连AO,已知△AOB的面积为4。
轴,垂足为B,连AO,已知△AOB的面积为4。
(1)求反比例函数的解析式;
(2)若点A的纵坐标为4,过点A的直线与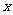 轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标;
轴交于P,且△APB与△AOB相似,求所有符合条件的点P的坐标;
(3)在(2)的条件下,过点P、O、A的抛物线是否可由抛物线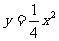 平移得到?若是,请说明由抛物线
平移得到?若是,请说明由抛物线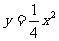 如何平移得到;若不是,请说明理由。
如何平移得到;若不是,请说明理由。

24.某食品批发部准备用10000元从厂家购进一批出厂价分别为16元/箱和20元/箱的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).
(1)求所获销售利润y(元)与x(箱)之间的函数关系式;
(2)根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com