

3.在数轴上表示-12的点与表示-3的点的距离是( )
A.9 B.-9 C.13 D.-13
2.已知一个数的绝对值等于2,那么这个数为( )
A.2 B.2 或 -2 C.-2 D.|2|
1.下面两个数互为相反数的是 ( )
A.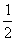 和 0.2
B.
和 0.2
B.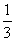 和 -0.333 C.
和 -0.333 C.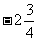 和
和 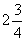 D.9 和
D.9 和 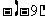
26.(12分)如图,在平面直角坐标系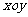 中,M是
中,M是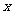 轴正半轴上一点,⊙M与
轴正半轴上一点,⊙M与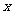 轴的正半轴交于A、B两点,A在B的左侧,且OA,OB的长是方程
轴的正半轴交于A、B两点,A在B的左侧,且OA,OB的长是方程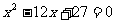 的两根,ON是⊙M的切线,N为切点,N在第四象限。
的两根,ON是⊙M的切线,N为切点,N在第四象限。
(1)求⊙M的直径。
(2)求直线ON的解析式。
(3)在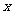 轴上是否存在一点T,使△OTN是等腰三角形,若存在请在图2中标出T点所在位置,并画出△OTN(要求尺规作图,保留作图痕迹,不写作法,不证明,不求T的坐标);若不存在,请说明理由。
轴上是否存在一点T,使△OTN是等腰三角形,若存在请在图2中标出T点所在位置,并画出△OTN(要求尺规作图,保留作图痕迹,不写作法,不证明,不求T的坐标);若不存在,请说明理由。
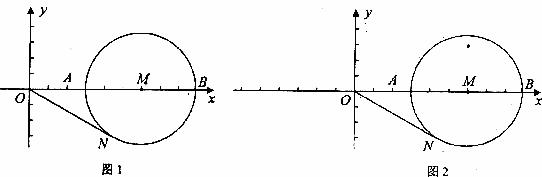
25.(10分)如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽(部分参考数据:322=1024,522=2704,482=2304)。
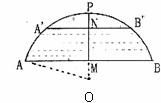
24.(10分)如下图所示,有一座圆弧形拱桥,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施;若拱顶离水面只有4米,即PN=4米时,是否应采取紧急措施?
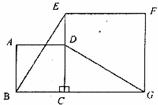
23.(9分)如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG。
(1)观察猜想BE与DG之间的大小关系,并证明你的结论。
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,请说明理由。
22.(9分)有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图)。小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张。
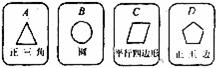
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌面图形都是中心对称图形的纸牌的概率。
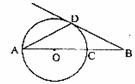
21.(6分)如图,线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B=30°,边BD交圆于点D,试判断B D与⊙O的位置关系,并说明理由。
20.(5分)小明运用公式法解一元二次方程 ,他认为此时的
,他认为此时的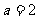 ,
,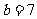 ,
,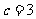 ,则有
,则有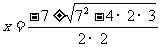 ,但小亮认为小明做错了,你知道其中错在哪里吗?请你指出来并写出正确的解法。
,但小亮认为小明做错了,你知道其中错在哪里吗?请你指出来并写出正确的解法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com