2、请根据要求完成以下两个成语题(6分)

(1)解释“鹤立鸡群”，写出一个含有“鹤”字的成语，再用“鹤立鸡群”造句。(3分)　　

①解释：　　　　　　　　　　　　　　　　　　　　　　　　　　

②成语：　　　　　　　　　　　　　　　　　　　　　　　　　　

③造句：　　　　　　　　　　　　　　　　　　　　　　　　　 　

　　 (2)请写出与成语“三顾茅庐”有关的人物，写出两个以上“三”字开头的成语，再用“三顾茅庐”造句。(3分)

①人物：　　　　　　　　　　　　　　　　　　　　　　　　　　

②成语：　　　　　　　　　　　　　　　　　　　　　　　　　　

③造句：　　　　　　　　　　　　　　　　　　　　　　　　　　

1、请根据拼音写出汉字或给加点字注音。(4分)

我希望他们不再像我，又大家隔膜(　　 )(　　 )起来，……然而我又不愿意他们因为要一气，都如我的辛苦展转而生活，也不愿意他们都如闰土的辛苦麻木而生活，也不愿意都如别人的辛苦zì ( 　　)s u ī(　　 )而生活。

24． (本题满分14分)如图，已知抛物线y = ax² + bx－3与x轴交于A、B两点，与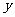轴交于C点，经过A、B、C三点的圆的圆心M(1，m)恰好在此抛物线的对称轴上，⊙M的半径为．设⊙M与y轴交于D，抛物线的顶点为E．

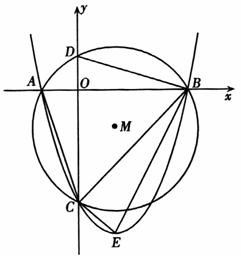
(1)求m的值及抛物线的解析式；

(2)设∠DBC = a，∠CBE = b，求sin(a－b)的值；

(3)探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．

23．(本题满分12分)如图，等边三角形ABC的面积为1，将其三边AC，CB，BA分别延长到B′，A′，C′，使．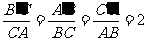

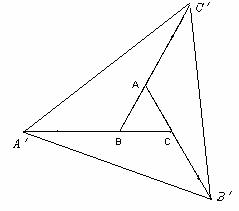
(1)　　　 试判断△A′B′C′的形状，并说明理由．

(2)　　　 △A′BC′可以通过怎样的几何变换(平移、旋转、轴对称或它们的组合)与△C′AB′重合？

　(3)求△A′B′C′的面积．

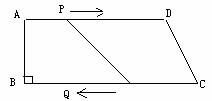
22．(本题满分12分) 如图，四边形ABCD是直角梯形，∠B=90°，AB=8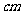，AD=24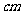，BC=26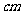，点P从A出发，以1的速度向D运动，点Q从C同时出发，以3 的速度向B运动.其中一个动点到达端点时，另一个动点也随之停止运动。从运动开始，经过多少时间，四边形PQCD成为平行四边形？成为等腰梯形？

21． (本题满分12分) 数学课上，年轻的刘老师在讲授“轴对称”时，设计了如下四种教学方法：

①教师讲,学生听；　　 ②教师让学生自己做；

③教师引导学生画图，发现规律；

④教师让学生对折纸，观察发现规律，然后画图．

数学教研组长将上述教学方法作为调研内容发到全年级8个班420名同学手中，要求每位同学选出自己最喜欢的一种，他随机抽取了60名学生的调查问卷，统计如图：

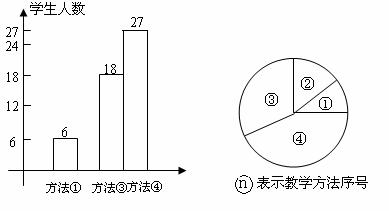
(1)请将条形统计图补充完整，并计算扇形统计图中方法③的圆心角．

(2)全年级同学中最喜欢的教学方法是哪一种？选择这种教学方法的约有多少人？

(3)假如抽取的60名学生集中在某两个班，这个调查结果还合理吗？为什么？

(4)请你对老师的教学方法提出一条合理化的建议．

20．(本题10分)请你依据下面图框中的寻宝游戏规则，探究“寻宝游戏”的奥秘：

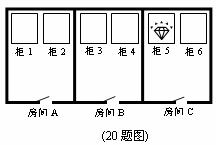
(1)用树状图表示出所有可能的寻宝情况；

(2)求在寻宝游戏中胜出的概率．

19．(本题10分)某校准备组织210名学生到我市著名的旅游景区“大纹流”草场进行野外考察活动，行李共有80件．学校计划租用甲、乙两种型号的汽车共6辆，经了解，甲种汽车每辆最多能载40人和10件行李，乙种汽车每辆最多能载30人和20件行李．

(1)设租用甲种汽车辆，请你帮助学校设计所有可能的租车方案；

(2)如果甲、乙两种汽车每辆的租车费用分别为1000元、800元，请你选择最省钱的一种租车方案．

18. (本题共2小题，每小题6分，共12分)

(1)计算：．

(2)化简：，并指出x的取值范围．