6．计算：(一3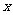²)·()=_____________．

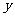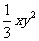5．在拼图游戏中，从下图(1)的四张纸片中，任取两张纸片，能拼成“小房子”如(2)的概率等于(　　 )．

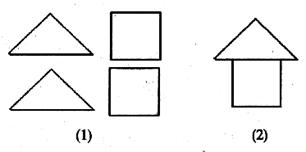
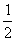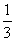A．l　 　　　　　 B． 　　　　　　　　 C．　 　　　　 D．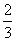

4．桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由(　 )个这样的正方体组成．

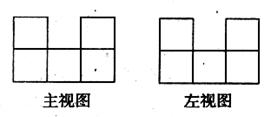
A．11　　 　　　　　　 B．12　 　　　　　　　 C．13　　 　　　　　　 D．14

3．小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还．”如果用纵轴y表示父亲与儿子行进中离家的距离，用横轴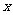表示父亲离家的时间，那么下面的图像与上述诗的含义大致吻合的是(　　 )．

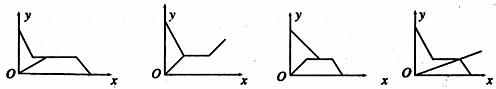
　　　　 A　　　　　　　　　　 B　　　　　　　 C　　　　　　　　 D

2．下列调查工作需采用普查方式的是(　　 )．

　　 A．环保部门对淮河某段水域的水污染情况的调查

　　 B．电视台对正在播出的某电视节目收视率的调查

　　 C．质检部门对各厂家生产的电池使用寿命的调查

　　 D．企业在给职工做工作服前进行尺寸大小调查

1．“太阳能”是一种既无污染又节省地下能源的能量，据科学家统计，平均每平方千米的地面一年从太阳获得的能量，相当于燃烧130000000千克的煤所产生的能量，用科学记数法表示这个数是(　　 )千克．

A．1.3×10⁸　　 　　　　　 B．13×10⁷　 　　　　 C．0.13×10⁹ 　　　　 D．1.3×10⁹

25．(本题12分)

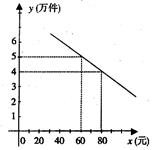
　　 某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支(不含进价)总计120万元．在销售过程中发现，年销售量y(万件)与销售单价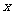 (元)之间存在着如图所示的一次函数关系．

　　 (1)求y关于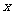的函数关系式；(5分)　

　　 (2)试写出该公司销售该种产品的年获利z(万元)关于销售单价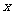 (元)的函数关系式，当销售单价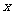为何值时，年获利最大?并求这个最大值．(7分)

24．(本题12分)

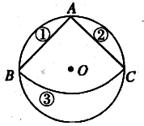
如图，从一个直径是2的圆形铁皮中剪下一个圆心为90°的扇形。

　 (1)求这个扇形的面积(结果保留)；(4分)　　

　　 (2)在剩下的三块余料中，能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由．(4分)

　　 (3)当圆O的半径R(R>0)为任意值时，(2)中的结论是否仍然成立?请说明理由。(4分)

23．(本题10分)

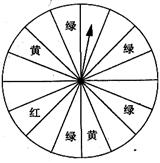
　　 在一次促销活动中，某商场为了吸引顾客，设立了一个可以自由转动的转盘，如图所示，转盘被平均分成16份，并规定：顾客每购买100元的商品，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得50元、30元、20元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可以直接获得购物券10元．

　　 (1)求每转动一次转盘所获购物券金额的平均数；(6分)

　　 (2)如果你在该商场消费125元，你会选择转转盘还是直接获得购物券?说明理由。(4分)

22．(本题12分)

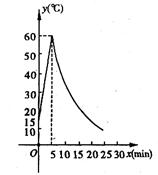
　　 制作一种产品，需先将材料加热达到60℃后，再进行操作，设该材料温度为y(℃)，从加热开始计算的时间为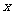(min)．据了解，设该材料加热时，温度y与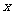时间成一次函数关系；停止加热进行操作时，温度y与时间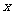成反比例关系(如图)．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．

　　 (1)分别求出将材料加热和停止加热进行操作时，y与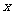函数关系式；(6分)

　　 (2)根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？(6分)