1．根据汉语拼音写出汉字。(4分)

①寥　　 (kuò)　 ②尴　　　 (gà)　 ③执　　　 (niù)　 ④　　　 (yùn)絮

25．(本题10分l

两条平行直线上各有n个点，用这n对点按如下规则连接线段：

①平行线之间的点在连线段时，可以有共同的端点，但不能有其他交点；

②符合①要求的线段须全部画出．

图(1)展示了当n=1时的情况，此时图中三角形的个数为0；

图(2)展示了当n=2时的情况，此时图中三角形的个数为2．

(1)当n=3时，请在图(3)中画出使三角形个数最少的图形，此时图中三角形的个数为___________．(5分)

　　 (2)试猜想当有n对点时，按上述规则画出的图形中，最少有多少个三角形？(3分)

　 (3)当n=2008时，按上述规则画出的图形中，最少有多少个三角形?(2分)

24．(本题10分)

　　 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格出售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．

　　 (1)求平均每天销售量y(箱)与销售价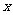(元／箱)之间的函数关系式；(3分)

　　 (2)求平均每天的销售利润w(元)与销售价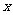 (元／箱)之间的函数关系式；(3分)

　　 (3)当每箱苹果的销售价为多少时，可以获得最大利润?最大利润是多少?(4分)

23．(本题12分)

　　 如图，已知在梯形ABCD中，AD//BC，AB=DC，对角线AC和BD相交于点D，E是BC边上一个动点(层点不与B、C两点重合)，EF//BD交AC于点F，EG//AC交BD于点G

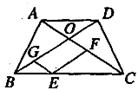
　　 (1)求证：四边形EFOG的周长等于2OB；(6分)

　　 (2)请你将上述题目的条件“梯形ABCD中，AD//BC，AB=DC”改为另一种四边形，其他条件不变，使得结论“四边形EFOG的周长等于2OB”仍成立，并将改编后的题目写出已知和求证．但不证明．(6分)

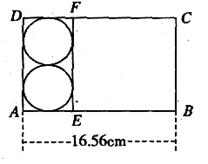
22．(本题10分)

　　 工厂用长方形的铁皮制作易拉罐，一张长方形铁皮根据下图中的数据下料，假设焊接的部分忽略不计，求这个易拉罐的容积．(取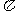=3.14，精确到0.01立方米)

21．(本题10分)

　　 甲、乙两人骑自行车前往A地，他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示，请根据图像所提供的信息解答下列问题：

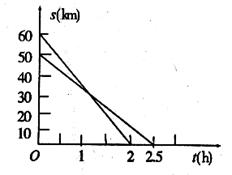
(1)甲、乙两人的速度各是多少?(4分)

　　 (2)写出甲、乙两人距A地的路程s与行驶时间I之间的函数关系式(任写一个)；(3分)

　　 (3)在什么时间内乙比甲离A地更近?(3分)

20．(本题10分)

将背面相同，正面分别标有数字1、2、3、4的四张卡片洗匀后，背面朝上放在桌面上．

(1)从中随机抽取一张卡片，求该卡片正面朝上的数字是偶数的概率；(5分)

(2)先从中随机抽取一张卡片(不放回)，将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明．(5分)

19．(本题10分)

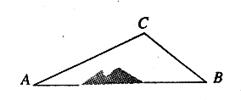
　　 如图，A、B两地之间有一座山，汽车原来从A地到B地须经过C地沿折线A-C-B行驶，已知AC=10km，∠A=30°，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走多少千米?(结果精确到0.1km)

18．(本题10分)：

　　 如图，已知二次函数的图像经过点A和点B．

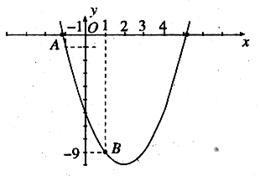
　　 (1)求该二次函数的表达式；(4分)

　　 (2)写出该抛物线的对称轴及顶点坐标；(2分)

　　 (3)点P(m，m)与点Q均在该函数图像上，(其中m>0)，且这两点关于抛物线的对称轴对称，求m的值及点Q到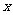轴的距离．(4分)

17．(本题10分)

　　 某学校举行演讲比赛，选出了10名同学担任评委，并事先拟订从如下4个方案中选择合理的方案来确定演讲者的最后得分(满分为10分)：

　　 方案l：所有评委所给的平均分．

　　 方案2：在所有评委所给的分中，去掉最高分和最低分，然后再计算其余给分的平均数．

　　 方案3：所有评委所给分的中位数．

　　 方案4：所有评委所给分的众数．

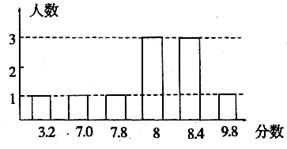
　　 为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验，下图是这个同学的得分统计图．

　　 (1)分别按上述4个方案计算这个同学演讲的最后得分；(8分)　

　　 (2)根据(1)中的结果，请用统计的知识说明哪些方案不合适作为这个同学演讲的最后得分．(2分)