
9、 . 10、 .
 24.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
24.如图,将边长为4的正方形纸片,置于平面直角坐标系内,顶点A在坐标原点,AB在x轴正方向上,E、F分别是AD、BC的中点,M在DC上,将△ADM沿折痕AM折叠,使点D折叠后恰好落在EF上的P点处.
(1)求点M、P的坐标;
(2)求折痕AM所在直线的解析式.
(3)设点H为直线AM上的点,是否存在这样的点H,
使得以H、A、P为顶点的三角形为等腰三角形,
若存在,请直接写出点H的坐标;若不存在,请说明理由.
(第24题图)
线 l 的对称点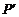 的坐标为 (不必证明);
(第23题图)
的坐标为 (不必证明);
(第23题图)
(3)已知两点D(1,-3)、E(-1,-4),试在直线 l 上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
们的坐标: 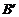 、
、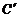 ;
;
(2)结合图形观察以上三组点的坐标,你会发现:坐
关于直线 l 的对称点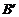 、
、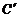 的位置,并写出他
的位置,并写出他
(1)由图观察易知A(0,2)关于直线l的对称点 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)
(2)求图中阴影部分的面积(其中л≈3,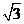 ≈1.7) 。
≈1.7) 。
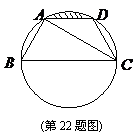 如图,已知点
如图,已知点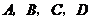 均在已知圆上,
均在已知圆上,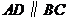 ,
, 平分
平分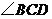 ,
, ,四边形
,四边形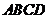 的周长为
的周长为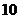 cm.
cm.
(1)求此圆的半径;
22. (本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com