
例5.(08年全国Ⅰ)在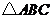 中,
中,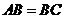 ,
,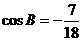 .若以
.若以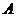 ,
,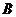 为焦点的椭圆经过点
为焦点的椭圆经过点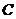 ,则该椭圆的离心率
,则该椭圆的离心率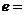 .
.
【点评】我们知道,在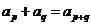 中,取
中,取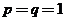 ,得
,得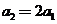 ;取
;取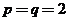 ,得
,得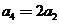 ,等等.这种取特殊值的方法,显示是由一般到特殊的思维方式.事实上,本题的数列
,等等.这种取特殊值的方法,显示是由一般到特殊的思维方式.事实上,本题的数列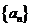 当中,隐含了子数列是等比数列,你能写出一般的通项公式吗?
当中,隐含了子数列是等比数列,你能写出一般的通项公式吗?
【解析】由题意,得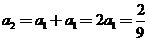 ,
,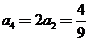 ,
,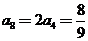 ,
,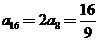 ,
,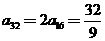 ,∴
,∴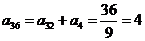 ,从而应当填
,从而应当填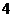 .
.
例4.(07年江西)已知数列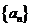 对于任意
对于任意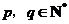 ,有
,有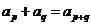 ,若
,若 ,则
,则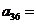 .
.
∴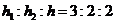 .
.
设正三棱柱的各棱长为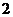 ,则
,则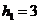 ,
,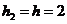 ,
,
【解析】由于所求的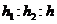 为定值,所以可将三棱柱特殊化为直三棱柱.又三棱锥、四棱锥的底面边长和侧棱都相等,所以取三棱柱为各棱长都相等的正三棱柱.
为定值,所以可将三棱柱特殊化为直三棱柱.又三棱锥、四棱锥的底面边长和侧棱都相等,所以取三棱柱为各棱长都相等的正三棱柱.
例3.(07年海南、宁夏)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为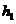 ,
,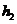 ,
,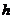 ,则
,则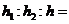 ___________.
___________.
所以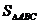 的最大值为
的最大值为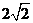 .
.
【点评】本题直接用“形”有一定的难度,若利用“数”运算,建立直角坐标系求解,则问题利于解决.这正好体现出“数形结合”思想,也进一步验证了
一个结论在一般情形下成立,在特殊情形下必成立。填空题只要结果,不要过程,所以当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可将填空题中的一般情形特殊化(将图形、图形的位置特殊化或给字母赋于特殊值等)再求解,这种解填空题的方法, 叫特殊化法。凡在一般情形下探求结论的填空题,都可用特例法。
∴当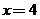 时,
时,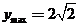 ,此时
,此时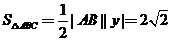 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com