22．(本题满分10分)

(1)探究新知：

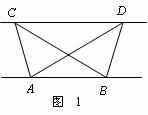
如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．

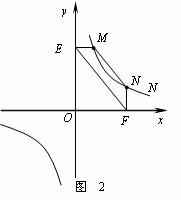
(2)结论应用：① 如图2，点M，N在反比例函数(k＞0)的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．

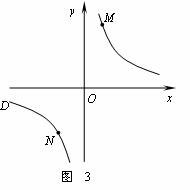
② 若①中的其他条件不变，只改变点M，N 的位置如图3所示，请判断 MN与EF是否平行．

21．(本题满分10分)　

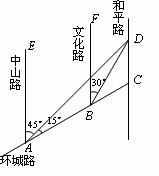
如图，AC是某市环城路的一段，AE，BF，CD都是南北方向的街道，其与环城路AC的交叉路口分别是A，B，C．经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上，AB＝2km，∠DAC＝15°．

(1)求B，D之间的距离；(2)求C，D之间的距离．

20．(本题满分10分)

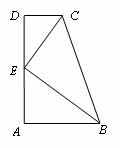
在梯形ABCD中，AB∥CD，∠A=90°， AB=2，BC=3，CD=1，E是AD中点．

求证：CE⊥BE． 　

19．(本题满分8分)　

为迎接2008年奥运会，某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”．该厂主要用甲、乙两种原料，已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒，生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒．该厂购进甲、乙原料的量分别为20000盒和30000盒，如果所进原料全部用完，求该厂能生产奥运会标志和奥运会吉祥物各多少套？　　

18．(本题满分8分)

振兴中学某班的学生对本校学生会倡导的“抗震救灾，众志成城”自愿捐款活动进行抽样调查，得到了一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3︰4︰5︰8︰6，又知此次调查中捐款25元和30元的学生一共42人．

(1)他们一共调查了多少人？ 　

(2)这组数据的众数、中位数各是多少？　

(3)若该校共有1560名学生，估计全校学生捐款多少元？　

17．(本题满分6分)

先化简，再求值：

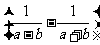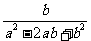÷，其中，．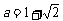　

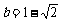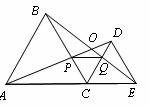
16．如图，C为线段AE上一动点(不与点A，E重合)，在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．以下五个结论：

① AD=BE；② PQ∥AE；③ AP=BQ；④ DE=DP；⑤ ∠AOB=60°．恒成立的有__________(把你认为正确的序号都填上)．

15．“上升数”是一个数中右边数字比左边数字大的自然数(如：34，568，2469等)．任取一个两位数，是 “上升数”的概率是　　　　　 ．

14．将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，结果如下表：

则a_n＝　　　　　 (用含n的代数式表示)．

13．某书店把一本新书按标价的九折出售，仍可获利20%．若该书的进价为21元，则标价为 　　　　　．