
2.下列计算中,正确的是
A.2a3-3a=-a; B.(-ab)2=-a2b2;
C.a2·a-3=a-1; D.-2a3÷(-2a)=-a2.
1.2的绝对值是
A. 2 B. -2 C. 0.5 D. -0.5
26.(本小题满分3分)
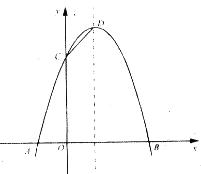
如图,已知抛物线与 轴交于A(-1,0)、B(3,0)两点,与
轴交于A(-1,0)、B(3,0)两点,与 轴交于点C(0,3)。
轴交于点C(0,3)。
(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形,若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
(3)若点M是抛物线上一点,以B、C,D、M为顶点的四边形是直角梯形,试求出点M的坐标。
25.(本小题满分11分)
已知∠MAN,AC平分∠MAN。
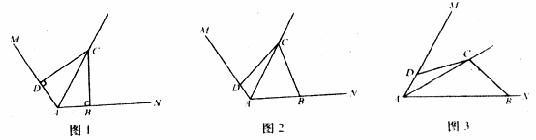
(1)在图1中,若∠MAN=120º,∠ABC=∠ADC=90º,求证AB+AD=AC;
(2)在图2中,若∠MAN=120º,∠ABC+∠ADC=180º,则(1)中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在图3中
①若∠MAN=60º,∠ABC+∠ADC=180º,则AB+AD= AC;
②若∠MAN=α(00<α<180º),∠ABC+∠ADC=180º,则AB+AD= AC(用含 的三角函数表示),并给出证明。
的三角函数表示),并给出证明。
24.(本小题满分10分)
某商场欲购进A、B两种品牌的饮料共500箱,此两种饮料每箱的进价和售价如下表所示。设购进A种饮料 箱,且所购进的两种饮料能全部卖出,获得的总利润为
箱,且所购进的两种饮料能全部卖出,获得的总利润为 元。
元。
|
品牌 |
A |
B |
|
进价(元/箱) |
55 |
35 |
|
售价(元/箱) |
63 |
40 |
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能获利最多?并求出最大利润。(注:利润=售价-进价)
23.(本小题满分9分)
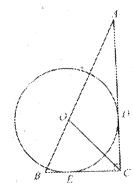
如图,Rt△ABC中,∠ACB=90º,AC=4,BC=2,以AB上的一点O为圆心的圆分别与AC、BC相切与点D、E。
(1)求⊙O的半径;
(2)求sin∠BOC得值。
22.(本小题满分7分)
在某道路拓宽改造工程中,一工程队承担了24千米的任务,为了减少施工带来的影响,在确保工程质量的前提下,实际施工速度是原计划的1.2倍,结果提前20天完成任务,求原计划平均每天改造道路多少千米?
21.(本小题满分7分)
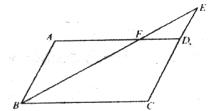
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=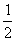 CD。
CD。
(1)求证:△ABF∽△CEB,
(2)若DEF的面积为2,求□ABCD得面积。
20.(本小题满分6分)
某油桃种植户今年喜获丰收,他从采摘的一批总质量为900千克的油桃中随机抽取了10个油桃,称得其质量(单位:克)分别为:106,99,100,113,111,97,104,112,98,110。
(1)估计这批油桃中每个油桃的平均质量;
(2)若质量不小于110克的油桃可定为优级,估计这批油桃中,优级油桃占油桃总数的百分之几?达到优级的油桃有多少千克?
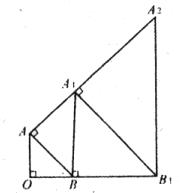
19.如图,以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1,再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1,如此作下去。若OA=OB=1,则第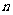 个等腰直角三角形的面积
个等腰直角三角形的面积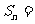 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com