
8. 一交通管理人员星期天在市中心的某十字路口,对闯红灯的人次进行统计,根据上午7∶00 ~ 12∶00中各时间段(以1小时为一个时间段)闯红灯的人次,制作了如图所示的条形统计图,则各时间段闯红灯人次的众数和中位数分别为
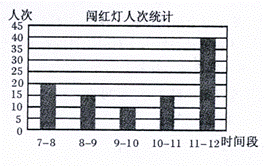
A.15,15 B.10,15 C.15,20 D.10,20
7. 如图,在△ABC与△DEF中,已有条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是

A.∠B=∠E,BC=EF B.BC=EF,AC=DF
C.∠A=∠D,∠B=∠E D.∠A=∠D,BC=EF
6. 在函数y=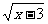 中,自变量x的取值范围是
中,自变量x的取值范围是
A.x≥ - 3 B.x≤ - 3 C.x≥ 3 D.x≤ 3
5. 下列事件是必然事件的是
A.打开电视机,任选一个频道,屏幕上正在播放天气预报
B.到电影院任意买一张电影票,座位号是奇数
C.在地球上,抛出去的篮球会下落
D.掷一枚均匀的骰子,骰子停止转动后偶数点朝上
4. 用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是
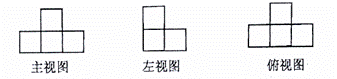
A.4 B.5 C.6 D.7
3. 北京奥运会火炬传递以“和谐之旅”为主题,以“点燃激情 传递梦想”为口号进行,其传递总路程约为1370000千米,这个路程用科学计数法表示为
A.13.7×104千米 B.13.7×105千米 C.1.37×105千米 D.1.37×106千米
2. 化简( - 3x2)·2x3的结果是
A.- 6x5 B.- 3x5 C.2x5 D.6x5
1. 2cos45°的值等于
A.  B.
B.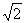 C.
C.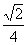 D.
D.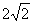
24.(本小题满分12分)
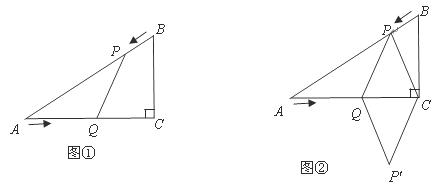
已知:如图①,在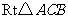 中,
中,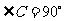 ,
,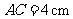 ,
,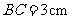 ,点
,点 由
由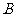 出发沿
出发沿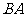 方向向点
方向向点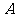 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点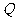 由
由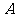 出发沿
出发沿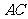 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接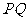 .若设运动的时间为
.若设运动的时间为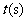 (
(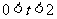 ),解答下列问题:
),解答下列问题:
(1)当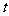 为何值时,
为何值时,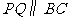 ?
?
(2)设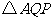 的面积为
的面积为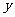 (
(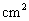 ),求
),求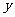 与
与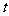 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻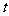 ,使线段
,使线段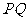 恰好把
恰好把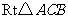 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时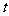 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)如图②,连接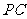 ,并把
,并把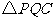 沿
沿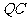 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻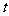 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
23.(本小题满分10分)
实际问题:某学校共有18个教学班,每班的学生数都是40人.为了解学生课余时间上网情况,学校打算做一次抽样调查,如果要确保全校抽取出来的学生中至少有10人在同一班级,那么全校最少需抽取多少名学生?
建立模型:为解决上面的“实际问题”,我们先建立并研究下面从口袋中摸球的数学模型:
在不透明的口袋中装有红、黄、白三种颜色的小球各20个(除颜色外完全相同),现要确保从口袋中随机摸出的小球至少有10个是同色的,则最少需摸出多少个小球?
为了找到解决问题的办法,我们可把上述问题简单化:
(1)我们首先考虑最简单的情况:即要确保从口袋中摸出的小球至少有2个是同色的,则最少需摸出多少个小球?
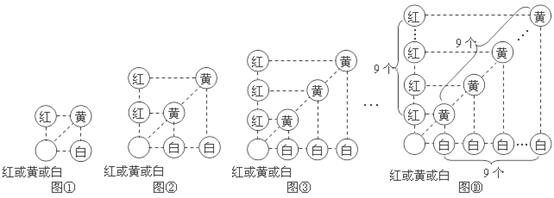
假若从袋中随机摸出3个小球,它们的颜色可能会出现多种情况,其中最不利的情况就是它们的颜色各不相同,那么只需再从袋中摸出1个小球就可确保至少有2个小球同色,即最少需摸出小球的个数是: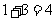 (如图①);
(如图①);
(2)若要确保从口袋中摸出的小球至少有3个是同色的呢?
我们只需在(1)的基础上,再从袋中摸出3个小球,就可确保至少有3个小球同色,即最少需摸出小球的个数是: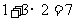 (如图②)
(如图②)
(3)若要确保从口袋中摸出的小球至少有4个是同色的呢?
我们只需在(2)的基础上,再从袋中摸出3个小球,就可确保至少有4个小球同色,即最少需摸出小球的个数是: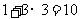 (如图③):
(如图③):

(10)若要确保从口袋中摸出的小球至少有10个是同色的呢?
我们只需在(9)的基础上,再从袋中摸出3个小球,就可确保至少有10个小球同色,即最少需摸出小球的个数是: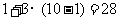 (如图⑩)
(如图⑩)
模型拓展一:在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各20分(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 ;
(2)若要确保摸出的小球至少有10个同色,则最少需摸出小球的个数是 ;
(3)若要确保摸出的小球至少有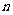 个同色(
个同色(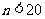 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
模型拓展二:在不透明口袋中装有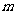 种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
种颜色的小球各20个(除颜色外完全相同),现从袋中随机摸球:
(1)若要确保摸出的小球至少有2个同色,则最少需摸出小球的个数是 .
(2)若要确保摸出的小球至少有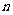 个同色(
个同色(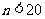 ),则最少需摸出小球的个数是 .
),则最少需摸出小球的个数是 .
问题解决:(1)请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型;
(2)根据(1)中建立的数学模型,求出全校最少需抽取多少名学生.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com