2．下列说法正确的是

(A)经过直线外一点有且只有一条直线与已知直线垂直

(B)经过一点，有且只有一条直线与这条直线平行

(C)三角形按边分为不等边三角形、等腰三角形和等边三角形

(D)两直线被第三直线所截，同位角相等

1．下列图形中，∠1与∠2是对顶角的是

29．(本小题10分)

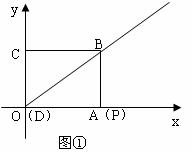
如图①，矩形ABCD的两条边在坐标轴上，点D与原点O重合，对角线BD所在的直线的函数关系式为y=x,AD=8。矩形ABCD沿DB方向以每秒1个单位长度运动，同时点P从点A出发做匀速运动，沿矩形ABCD的边经过点B到达点C，用了14秒。

(1)求矩形ABCD 的周长。

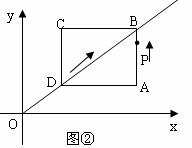
(2)如图②，图形运动到第5秒时，求点P的坐标。

(3)设矩形运动的时间为t，当0≤t≤6时，点P所经过的路线是一条线段，请求出线段所在直线的函数关系式。

(4)当点P在线段AB或BC上运动时，过点P作x轴、y轴的垂线，垂足分别为E、F，则矩形PEOF是否能与矩形ABCD相似(或位似)？若能，求出t的值；若不能，说明理由。

28．(本题8分)

原始问题：已知矩形A的长、宽分别是2和1，那么是否存在另一个矩形B，它的周长和面积分别是矩形A的周长和面积的2倍？

对上述问题，小明同学从“图形”的角度，利用函数知识给予了解决。

小明论证的过程开始是这样的：如果用x、y分别表示矩形的长和宽，那么矩形B满足x+y＝6，xy＝4。请你按照小明的论证思路完成后面的论证过程。

　　　 新的问题：已知矩形A的长和宽分别是2和1，那么是否存在一个矩形C，它的周长和面积分别是矩形A的周长和面积的一半？

小明认为这个问题是肯定的，你同意小明的观点吗？为什么？

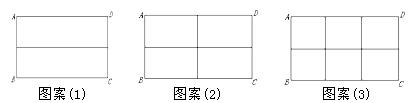
请根据以上图案回答下列问题:

(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,

长方形框架ABCD的面积是　　　 m²；

(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为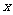m,长方形框架ABCD的面积为S＝　　　 (用含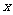的代数式表示)；当AB＝　　　 m时, 长方形框架ABCD的面积S最大；

(3)在图案(3)中,如果铝合金材料总长度为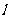m, 设AB为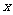m,求出ABCD的面积S与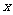的函数关系式，并求出当AB为多少m时, 长方形框架ABCD的面积S最大.

27．(本小题8分)

26．(本小题8分)

无锡新区某电子公司根据市场需求，在一天内计划生产A、B两种型号的电子产品共52件，该公司所筹生产此电子产品的资金不少于2710元，但不超过2794元，且所筹资金全部用于生产此两型电子产品，所生产的此两型电子产品可全部售出，此两型电子产品的生产成本和售价如下表：

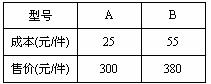
(1)该公司对这两型电子产品有哪几种生产方案？

(2)该公司如何生产能获得最大利润？

(3)根据市场调查，每件B型电子产品的售价不会改变，而每件A型电子产品的售价将会提高m元(m>40)，该厂应该如何生产可以获得最大利润？(注：利润＝售价－成本)

25．(本小题8分)

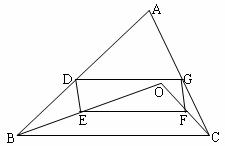
点O是△ABC所在平面内一动点，连接OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连接，如果DEFG能构成四边形。

(1)如图，当点O在△ABC内时，求证：四边形DEFG是平行四边形。

(2)当点O移动到△ABC外时，(1)的结论是否成立？画出图形并说明理由。

(3)若四边形DEFG为矩形，点O所在位置应满足什么条件？试说明理由。

24．(本小题6分)

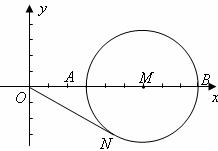
如图，在平面直角坐标系中，M是X轴正半轴上一点，⊙M与X轴的正半轴交于A、B两点，A在B的左侧，且OA、OB的长是方程x²-12x+27=0的两根，ON是⊙M的切线，N为切点，N在第四象限．

(1)求⊙M的直径．(2)求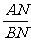的值．(3)求直线ON的解析式．

23．(本小题8分)

甲、乙两同学做“射任意球”的游戏，他们商定：每人玩5局，每局在距球门25米处将足球射入空门，一次不进可以射第二次，依次类推，但最多只能射6次，当球射进后，该局结束，并记下射门次数；当6次都未射进，该局也结束，并记为“×”，两人5局射门进球情况如下：

(1)为了计算得分，双方约定：记“×”的该局为0分，其他局得分的计算方法要满足以下两个条件：①射门次数越多，得分越低；②得分为正数。请你按约定的要求，用公式或文字叙述的方式，选取其中的一种写出一个将其他局的射门次数n换算成得分M的具体方案；

(2)根据上述约定和你写出的方案，请你通过表格的方式，统计甲、乙两人的每局得分和平均分，并从平均分的角度来判断甲、乙两人谁的任意球射门技术更精湛。