
1.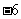 的相反数是 ,16的算术平方根是
.
的相反数是 ,16的算术平方根是
.
25.(本题12分)如图1,抛物线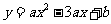 经过A(-1,0),C(3,2)两点,与
经过A(-1,0),C(3,2)两点,与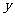 轴交于点D,与
轴交于点D,与 轴交于另一点B。
轴交于另一点B。
⑴求此抛物线的解析式;
⑵若直线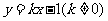 将四边形ABCD面积二等分,求
将四边形ABCD面积二等分,求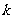 的值;
的值;
⑶如图2,过点E(1,-1)作EF⊥ 轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.
轴于点F,将△AEF绕平面内某点旋转180°后得△MNQ(点M,N,Q分别与点A,E,F对应),使点M,N在抛物线上,求点M,N的坐标.

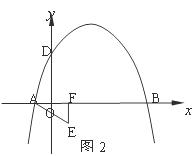
24.(本题10分)正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F。如图1,当点P与点O重合时,显然有DF=CF.
⑴如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E。
①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
⑵若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E。请完成图3并判断⑴中的结论①、②是否分别成立?若不成立,写出相应的结论(所写结论均不必证明)
23.(本题10分)某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件。市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件。设每件涨价 元(
元( 为非负整数),每星期的销量为
为非负整数),每星期的销量为 件.
件.
⑴求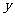 与
与 的函数关系式及自变量
的函数关系式及自变量 的取值范围;
的取值范围;
⑵如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
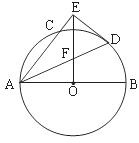
22.(本题8分)如图,AB是⊙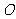 的直径,AC是弦,∠BAC的平分线AD交⊙
的直径,AC是弦,∠BAC的平分线AD交⊙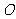 于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.⑴求证:DE是⊙
于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.⑴求证:DE是⊙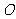 的切线;⑵若
的切线;⑵若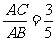 ,求
,求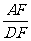 的值。
的值。
21.(本题7分)
⑴点(0,1)向下平移2个单位后的坐标是
,直线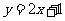 向下平移2个单位后的解析式是
;
向下平移2个单位后的解析式是
;
⑵直线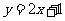 向右平移2个单位后的解析式是
;
向右平移2个单位后的解析式是
;
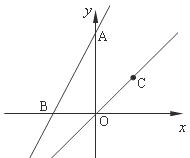
⑶如图,已知点C为直线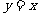 上在第一象限内一点,直线
上在第一象限内一点,直线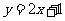 交
交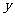 轴于点A,交
轴于点A,交 轴于B,将直线AB沿射线OC方向平移
轴于B,将直线AB沿射线OC方向平移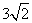 个单位,求平移后的直线的解析式.
个单位,求平移后的直线的解析式.
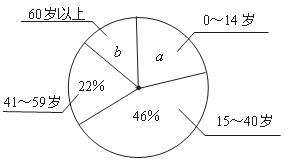
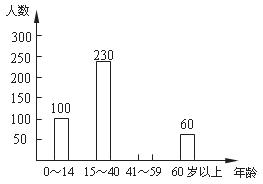
20.(本题7分)典典同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
请根据以上不完整的统计图提供的信息,解答下列问题:
⑴典典同学共调查了 名居民的年龄,扇形统计图中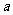 = ,
= ,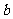 = ;
= ;
⑵补全条形统计图;
⑶若该辖区年龄在0-14岁的居民约有3500人,请估计年龄在15-59岁的居民的人数.
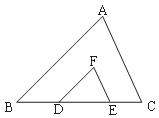
19.(本题6分)如图,点D,E在BC上,且FD∥AB,FE∥AC。求证:△ABC∽△FDE.
18.(本题6分)先化简,再求值: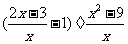 ,其中
,其中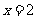 .
.
17.(本题6分)解方程: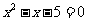 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com