1．－3的立方是

A．－27　　　　 　　　　 B．－9 　　　　　　　　 C．9　　　　　 　　　　　 D．27

24. 如图1，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为2，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n.

(1)请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明.

(2)求m与n的函数关系式，直接写出自变量n的取值范围.

　 (3)以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图2).在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD+CE=DE.

　 (4)在旋转过程中,(3)中的等量关系BD+CE=DE是否始终成立,若成立,请证明,若不成立,请说明理由.

23.(本题满分10分)

为了落实国务院副总理李克强同志到恩施考察时的指示精神,最近，州委州政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=－2x+80.设这种产品每天的销售利润为y(元).

(1)求y与x之间的函数关系式.

(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?

(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?

22.(本题满分9分)

如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC，过点D作DE⊥AC，垂足为E.

(1)求证：AB=AC；

(2)求证：DE为⊙O的切线；

(3)若⊙O的半径为5,∠BAC=60°,求DE的长.

21.(本题满分9分)

国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.为此,我州今年初中毕业生学业考试体育学科分值提高到40分,成绩记入考试总分.某中学为了了解学生体育活动情况,随机调查了720名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,所得的数据制成了如图的扇形统计图和频数分布直方图.

根据图示,解答下列问题:

(1)若在被调查的学生中随机选出一名学生测试其体育成绩,选出的恰好是“每天锻炼超过1小时”的学生的概率是多少？

(2)“没时间”的人数是多少？并补全频数分布直方图；

(3)2008年恩施州初中毕业生约为4.3万人,按此调查,可以估计2008年全州初中毕业生中每天锻炼未超过1小时的学生约有多少万人？

(4)请根据以上结论谈谈你的看法.

20. (本题满分8分)

如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.

(1)用含x的代数式表示AC+CE的长；

(2)请问点C满足什么条件时,AC+CE的值最小?

(3)根据(2)中的规律和结论,请构图求出代数式的最小值.

19.(本题满分8分)

手牵着手,心连着心.2008年5月12日发生在四川汶川的特大地震灾害,牵动着全中国人民的心.某校团支部发出为灾区捐款的倡议后,全校师生奉献爱心,踊跃捐款,已知全校师生共捐款 4万5千元,其中学生捐款数比老师捐款数的2倍少9千元,该校老师和学生各捐款多少元?

18.(本题满分8分)

如图，在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等，并说明理由.

17.(本题满分8分)

请从下列三个代数式中任选两个构成一个分式，并化简该分式

x－4xy+4y　　　 x－4y　　　　 x－2y

16. 如图,扇形OAB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的

底面半径为

A.　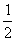 　　　　　B.　 　　　　　　　 C.　 　　　　　　　 D.