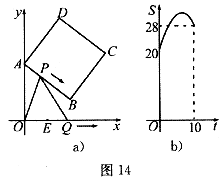
28．(本小题13分)如图14a，正方形ABCD的顶点A、B的坐标分别为(0，10)、(8，4)，顶点C、D在第一象限．点P从点A出发，沿正方形按逆时针方向匀速运动，同时，点Q从点E(4，0)出发，沿z轴正方向以相同速度运动．当点P到达点C时，P、Q两点同时停止运动，设运动的时间为．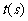

(1)求正方形ABCD的边长．

(2)当点P在AB边上运动时，△OPQ的面积S(平方单位)与时间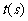之间的函数图像为抛物线的一部分(如图14b所示)，求P、Q两点的运动速度．

(3)求(2)中面积S(平方单位)与时间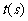的函数关系式及面积S取最大值时点P的坐标．

(4)若点P、Q保持(2)中的速度不变，则点P沿着AB边运动时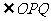，的大小随着时间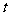的增大而增大；沿着BC边运动时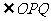，的大小随着时间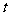的增大而减小．当点P沿着这两边运动时，使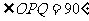的点P有　　　　　　　　　 个．

(抛物线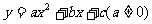的顶点坐标是)

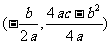27．(本小题9分)某同学根据某五个城市某年商品房销售均价(即销售平均价)的数据，绘制了统计图(图13)：

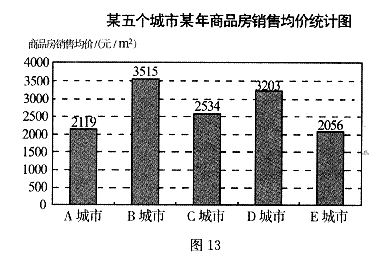
(1)这五个城市该年商品房销售均价的中位数、极差分别是多少?

(2)若2年前A城市的商品房销售均价为1600元／m²，试估计A城市从2年前到该年商品房销售均价的年平均增长率约是多少(要求误差小于1%)？

26．(本小题11分)某经销商销售了台湾水果凤梨，根据以往销售经验，每天的售价与销售量之间有如下关系：

设当单价从38元／kg 下调了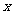元时，销售量为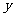kg；

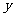(1)写出与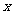间的函数关系式．

(2)如果凤梨的进价是20元／kg，某天的销售价定为30元／kg，问这天的销售利润是多少？

(3)目前两岸还未直接通航，运输要绕行，需耗时一周(7天)，凤梨最长的保存期为一个月(30天)，若每天售价不低于30元／kg，问一次进货最多只能是多少千克？

25．(本小题8分)如图12所示，在平行四边形ABCD中，E为BC边上一点，且AB＝AE．

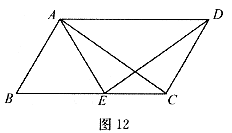
(1)求证：≌．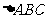

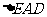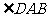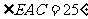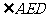(2)若AE平分，，求的度数．

24．(本小题10分)在学习勾股定理时，我们学会运用图(I)验证它的正确性：图中大正方形的面积可表示为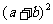，也可表示为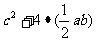，即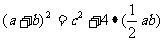由此推出勾股定理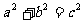，这种根据图形可以极简单地直观推论或验证数学规律和公式的方法，简称“无字证明”．

(1)请你用图(Ⅱ)(2002年国际数学家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等)．(3分)

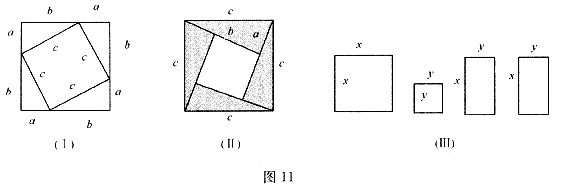
(2)请你用图(Ⅲ)提供的图形进行组合，用组合图形的面积表达式验证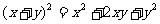：(3分)

(3)请你自己设计图形的组合，用其面积表达式验证：

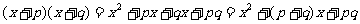　 (4分)

23．(本小题8分)某市长途客运站每天6︰30-7︰30开往某县的三辆班车，票价相同，但车的舒适程度不同．小张和小王因事需在这一时段乘车去该县，但不知道三辆车开来的顺序．两人采用不同的乘车方案：小张无论如何决定乘坐开来的第一辆车，而小王则是先观察后上车，当第一辆车开来时，他不上车，而是仔细观察车的舒适状况．若第二辆车的状况比第一辆车好，他就上第二辆车；若第二辆车不如第一辆车，他就上第三辆车．若按这三辆车的舒适程度分为优、中、差三等，请你思考并回答下列问题：

(1)三辆车按出现的先后顺序共有哪几种可能？

(2)请列表分析哪种方案乘坐优等车的可能性大？为什么？

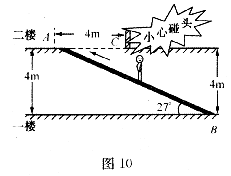
22．(本小题7分)如图10所示，某超市在一楼至二楼之问安装有电梯，天花板与地面平行．请你根据图中数据计算回答：小敏身高1.78m，她乘电梯会有碰头危险吗？姚明身高2.29m，他乘电梯会有碰头危险吗？

(可能用到的参考数值：)

20．(本小题8分)解分式方程：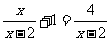

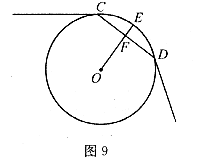
(本小题8分)如图9所示，一条公路的转弯处是一段圆弧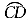，点O是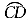的圆心，E为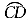上一点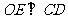，，垂足为F．已知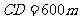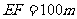，，求这段弯路的半径．

19．(本小题12分)

(1)计算：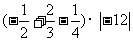

(2)计算：

18．在密码学中，直接可以看到内容为明码，对明码进行某种处理后得到的内容为密码．有一种密码，将英文26个字母以，b，c，…，z(不论大小写)依次对应1，2，3，…，26这26个自然数(见表格)．当明码对应的序号z为奇数时，密码对应的序号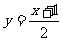；当明码对应的序号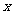为偶数时，密码对应的序号．

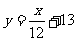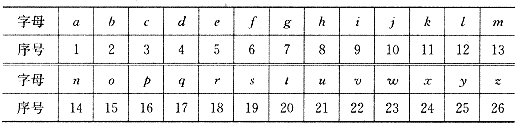
按上述规定，将明码“love”译成密码是　　　　　　　 ．