
3.下列运算正确的是( )
A.-2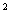 =4
B.2
=4
B.2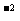 =-4
=-4
C. 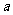 ·
·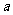
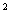 =
=
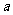
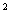 D.
D.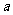 +2
+2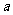 =3
=3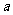
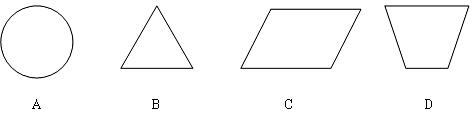
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
1.-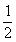 的相反数是( )
的相反数是( )
A.-2
B.2 C.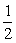 D.
D.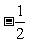
29.已知二次函数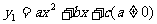 的图象经过三点(1,0),(-3,0),(0,
的图象经过三点(1,0),(-3,0),(0,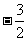 )。
)。
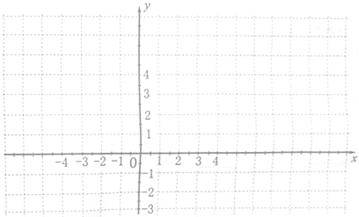
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分)
(2)若反比例函数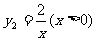 图像与二次函数
图像与二次函数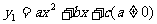 的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;(4分)
的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;(4分)
(3)若反比例函数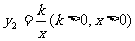 的图像与二次函数
的图像与二次函数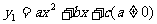 的图像在第一象限内的交点为A,点A的横坐标为
的图像在第一象限内的交点为A,点A的横坐标为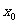 满足2<
满足2<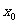 <3,试求实数k的取值范围。(5分)
<3,试求实数k的取值范围。(5分)
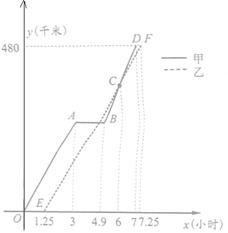
28.2008年5月12日14时28分四川汶川发生里氏8.0级强力地震。某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区。乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时)。图中的折线、线段分别表示甲、乙两组所走路程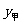 (千米)、
(千米)、 (千米)与时间x(小时)之间的函数关系对应的图像。请根据图像所提供的信息,解决下列问题:
(千米)与时间x(小时)之间的函数关系对应的图像。请根据图像所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了_________小时;(2分)
(2)甲组的汽车排除故障后,立即提速赶往灾区。请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(6分)
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不过25千米。请通过计算说明,按图像所表示的走法是否符合约定。
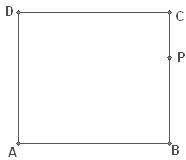
27.如图,在矩形ABCD中,AB=2,AD=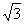 。
。
(1)在边CD上找一点E,使EB平分∠AEC,并加以说明;(3分)
(2)若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F。
①求证:点B平分线段AF;(3分)
②△PAE能否由△PFB绕P点按顺时针方向旋转而得到?若能,加以证明,并求出旋转度数;若不能,请说明理由。(4分)
26.已知关于x的不等式ax+3>0(其中a≠0)。
(1)当a=-2时,求此不等式的解,并在数轴上表示此不等式的解集;(4分)
(2)小明准备了十张形状、大小完全相同的不透明卡片,上面分别写有整数-10、-9、-8、-7、-6、-5、-4、-3、-2、-1,将这10张卡片写有整数的一面向下放在桌面上。从中任意抽取一张,以卡片上的数作为不等式中的系数a,求使该不等式没有正整数解的概率。(6分)
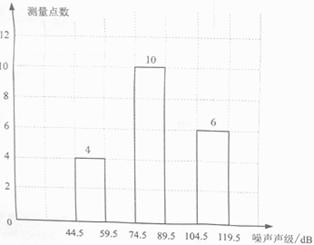
25.为了增强环境保护意识,6月5日“世界环境日”当天,在环保局工作人员指导下,若干名“环保小护士”组成了“控制噪声污染”课题学习研究小组.该小组抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位: dB ),将调查的数据进行处理(设所测数据均为正整数),得频数分布表如下:
|
组别 |
噪声声级分组 |
频数 |
频率 |
|
1 |
44.5~59.5 |
4 |
0.1 |
|
2 |
59.5~74.5 |
a |
0.2 |
|
3 |
74.5~89.5 |
10 |
0.25 |
|
4 |
89.5~104.5 |
b |
C |
|
5 |
104.5~119.5 |
6 |
0.15 |
|
合计 |
|
40 |
1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a=___________,b=____________,c=____________;(3分)
(2)补充完整频数分布直方图;(2分)
(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75 dB的测量点约有多少个?(4分)
24.如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan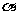 )为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。
)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。
(1)求完成该工程需要多少土方?(4分)
(2)该工程由甲、乙两个工程队同时合作完成,按原计划需要20天。准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率。甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成。问这两个工程队原计划每天各完成多少土方?(5分)
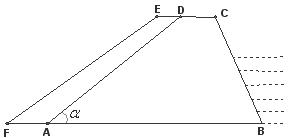
23.如图,⊿ABC内接于⊙O,AD是⊿ABC的边BC上的高,AE是⊙O的直径,连接BE,⊿ABE与⊿ADC相似吗?请证明你的结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com