
24.(本题满分10分)
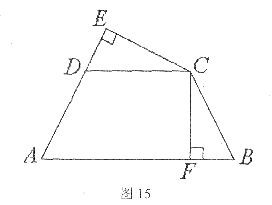
如图15,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB,垂足为F,∠A=∠B。
(1)写出图中相等的线段(已知的相等线段除外);
(2)选择(1)中你所写出的一组相等线段,说明它们相等的理由。
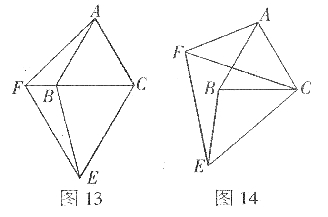
23.(本题满分10分)如图13,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE。
(1)线段AF和BE有怎样的大小关系?请证明你的结论;
(2)将图13中的△CEF绕点C旋转一定的角度,得到图14,(1)中的结论还成立吗?作出
判断并说明理由;
22.(本题满分9分)
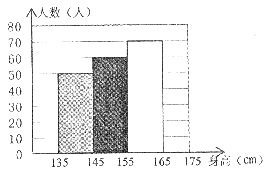
为了了解我县八年级女生的身高情况,在某校八年级女生中随机抽测了200名女生的身高,统计数据如下:
|
组别 |
身高(㎝) |
人数(人) |
|
|
第一组 |
135≤X<145 |
50 |
|
|
第二组 |
145≤X<155 |
P |
|
第三组 |
155≤X<165 |
70 |
|
第四组 |
165≤X<175 |
Q |
|
请你结合所给数据,回答下列问题:
(1)表中的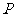 = ,
= , = 。
= 。
(2)请把直方图补充完整。
(3)请根据频数分布直方图画出扇形统计图。
21.(本题满分8分)
由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图12)。请你用四种不同的方法分别在图12中再将两个空白的小正方形涂黑,使它成为轴对称图形。


20.(本题满分8分)
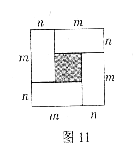
图10是一个长为2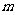 、宽为2
、宽为2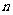 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图11的形状拼成一个正方形。
的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图11的形状拼成一个正方形。
(1)你认为图11中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图10中阴影部分的面积。
(3)观察图11你能写出下列三个代数式之间的等量关系吗?
代数式: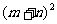 ,
, ,
,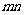 。
。
(4)根据(3)题中的等量关系,解决如下问题:
若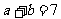 ,
,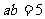 ,求
,求 和
和
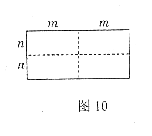
19.(本题满分9分)
(1)先化简,再求值: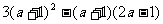 ,其中
,其中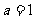 。
。
(2)已知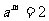 ,
,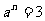 ,求
,求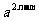 的值。
的值。
(3)利用分解因式计算:
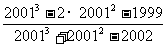
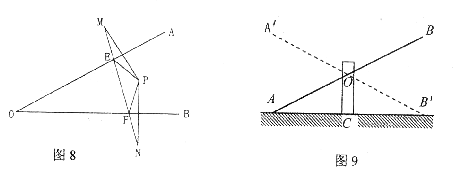
18.如图9,是跷跷板的示意图,支柱OC与地面垂直,点O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,△OAC=20°,横板上下可转动的最大角度(即∠A´OA)是 。
17.如图8,点P在△AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段心交OA、OB于点E、F,若△PEF的周长是20㎝,则线段MN的长是 。
16.在平面直角坐标系中,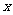 轴上一动点
轴上一动点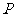 到定点
到定点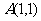 、
、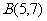 的距离分别为AP和BP,那么当BP+AP最小时,P点坐标为 。
的距离分别为AP和BP,那么当BP+AP最小时,P点坐标为 。
15.如图7,从边长为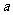 的大正方形纸板中挖去一个边长为
的大正方形纸板中挖去一个边长为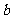 的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算阴影部分的面积可以验证公式 。
的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算阴影部分的面积可以验证公式 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com