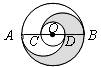
8．如图，在以O为圆心的两个同心圆中，大圆的直径AB交小圆于C、D两点，AC＝CD＝DB，分别以C、D为圆心，以CD为半径作圆．若AB＝6cm，则图中阴影部分的面积为　　　　 cm²．

7．计算：－＝　　　　 ．

6．如图，AB∥CD，AD与BC相交于点O，OA＝4，OD＝6，则△AOB与△DOC的周长比是　　　　　 ．

5．写出一个含有字母x、y的四次单项式　　　　　　 ．

4．学校团委组织九年级的共青团员参加植树活动，七个团支部植树的棵数为：16，13，15，16，14，17，17，则这组数据的中位数是　　　 ．

3．“x的2倍与5的差小于0”用不等式表示为　　　　　 ．

2．分解因式：2a²－4ab＝　　　　　　 ．

1．－6的绝对值是　　　 ．

25、(本题满分12分)

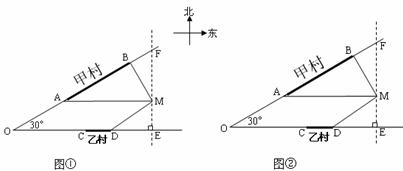
某县社会主义新农村建设办公室，为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题，想在这三个地方的其中一处建一所供水站，由供水站直接铺设管道到另外两处。

如图，甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计)，点M表示这所中学。点B在点M的北偏西30°的3km处，点A在点M的正西方向，点D在点M的南偏西60°的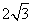km处。

为使供水站铺设到另两处的管道长度之和最短，现有如下三种方案：

方案一：供水站建在点M处，请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值；

方案二：供水站建在乙村(线段CD某处)，甲村要求管道铺设到A处，请你在图①中，画出铺设到点A和点M处的管道长度之和最小的线路图，并求其最小值；

方案三：供水站建在甲村(线段AB某处)，请你在图②中，画出铺设到乙村某处和点M处的管道长度之和最小的线路图，并求其最小值。

综上，你认为把供水站建在何处，所需铺设的管道最短？

24、(本题满分10分)

　 如图，矩形ABCD的长、宽分别为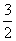和1，且OB＝1，点E(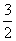，2)，连接AE、ED。

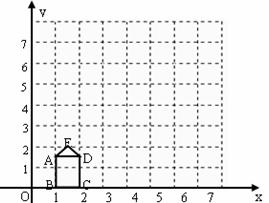
　 (1)求经过A、E、D三点的抛物线的表达式；

　 (2)若以原点为位似中心，将五边形AEDCB放大，使放大后的五边形的边长是原五边形对应边长的3倍，请在上图网格中画出放大后的五边形A′E′D′C′B′；

　 (3)经过A′、E′、D′三点的抛物线能否由(1)中的抛物线平移得到？请说明理由。