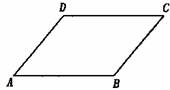
2．如图，在平行四边形ABCD中，∠A=50°，求∠C的度数。(5分)

1．计算：2x+3x-4x.(5分)

26．(12分)如图，AB是⊙O的直径，点C在⊙O上，∠BOC＝108°，过点C作直线CD分别交直线AB和⊙O于点D、E，连接OE，DE＝AB，OD＝2．

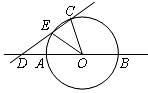
(1)求∠BDC的度数；

(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形．它的腰长与底边长的比(或者底边长与腰长的比)等于．

①写出图中所有的黄金三角形，选一个说明理由；

②求弦CE的长；

③在直线AB或CD上是否存在点P(点C、D除外)，使△POE是黄金三角形？若存在，画出点P，简要说明画出点P的方法(不要求证明)；若不存在，说明理由．

附加题：(本题满分10分)

温馨提示：同学们做完上面试题后，再认真检查一遍，估计一下你的得分。如果全卷得分低于90分，请继续完成下面试题。

25．(12分)如图，抛物线y＝x²+bx－2与x轴交于A、B两点，与y轴交于C点，且A(－1，0)．

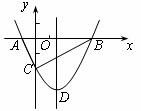
　　　 (1)求抛物线的解析式及顶点D的坐标；

(2)判断△ABC的形状，证明你的结论；

(3)点M(m，0)是x轴上的一个动点，当CM+DM的值最小时，求m的值．

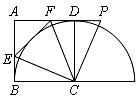
24．(10分)如图，在正方形ABCD中，E是AB边上任意一点，∠ECF＝45°，CF交AD于点F，将△CBE绕点C顺时针旋转到△CDP，点P恰好在AD的延长线上．

(1)求证：EF＝PF；

(2)直线EF与以C为圆心，CD为半径的圆相切吗？为什么？

23．(10分)为了支援四川汶川地震灾区人民重建家园，我市某校号召师生自愿捐款．已知第一次共捐款90000元，第二次共捐款120000元，第二次人均捐款额是第一次人均捐款额的1.2倍，捐款人数比比第一次多100人．问第一次和第二次捐款各多少元？

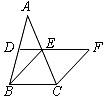
22．(10分)如图，在△ABC中，D、E分别是AB、AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连接CF．

(1)求证：四边形BCFE是菱形；

(2)若CE＝4，∠BCF＝130°，求菱形BCFE的面积(结果保留三个有效数字)．

20．(8分)如图，方格纸上的每个小正方形的边长均为1．

(1)观察图①、②中所画的“L”型图形，然后补画一个小正方形，使图①中所成的图形是轴对称图形，图②中所成的图形是中心对称图形；

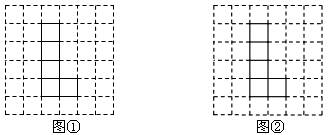
(2)补画后，图①、②中所成图形的是不是正方体的表面展开图(在括号内填“是”或“不是”)：

答：图①中的图形(　　 )，图②中的图形(　　 )．

19．(8分)已知一次函数y＝x+3的图象与反比例函数y＝都经过点A(a，4)．

(1)求a和k的值；

(2)判断点B(2，－)是否在该反比例函数的图象上．