
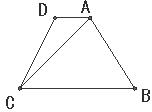
23.四边形一条对角线所在直线上的点,如果到这条对角线的两端点的距离不相等,但到另一对角线的两个端点的距离相等,则称这点为这个四边形的准等距点.如图l,点P为四边形ABCD对角线AC所在直线上的一点,PD=PB,PA≠PC,则点P为四边形ABCD的准等距点.
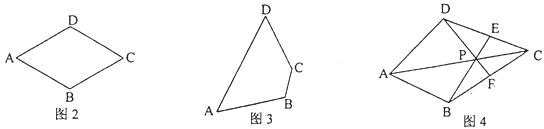
(1)如图2,画出菱形ABCD的一个准等距点.
(2)如图3,作出四边形ABCD的一个准等距点(尺规作图,保留作图痕迹,不要求写作法).
(3)如图4,在四边形ABCD中,P是AC上的点,PA≠PC,延长BP交CD于点E,延长DP交BC于点F,且∠CDF=∠CBE,CE=CF.求证:点P是四边形ABCD的准等距点.
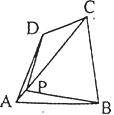
图1
22.(本小题满分4分)在平面直角坐标系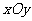 中,一次函数
中,一次函数 的图象l与
的图象l与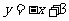 的图象关于y轴对称,直线l又与反比例函数
的图象关于y轴对称,直线l又与反比例函数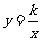 交于点
交于点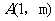 ,求m及k的值.
,求m及k的值.
21.(本小题满分5分)某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.小丽:如果以10元/千克的价格销售,那么每天可售出300千克.小强:如果以13元/千克的价格销售,那么每天可获取利润750元.小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)设该超市销售这种水果每天获取的利润为W元,那么当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?[利润=销售量×(销售单价-进价)]
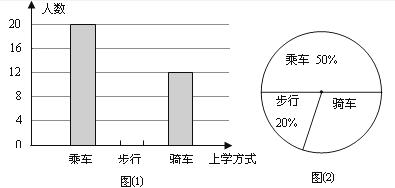
(2)在图(1)中,将表示“步行”的部分补充完整.
(3)在扇形统计图中,计算出“骑车”部分所对应的圆心角的度数.
(4)如果全年级共500名同学,请你估算全年级步行上学的学生人数.
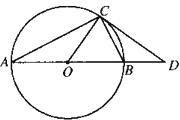
19.(本小题满分5分)已知:如图,AB是⊙O的直径,点C是⊙O上的一点,CD交AB的延长线于D,∠DCB=∠CAB.
(1) 求证:CD为⊙O的切线.
(2) 若CD=4,BD=2,求⊙O的半径长.
18.在梯形ABCD中,AD∥BC,AB=5,tanB=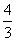 ,∠ACB=45
,∠ACB=45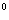 ,AD=2,求DC的长.
,AD=2,求DC的长.
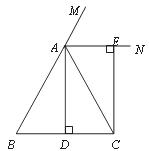
17.(本小题满分5分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
16.(本小题满分5分)已知2x-3=0,求代数式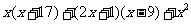 的值.
的值.
15.(本小题满分5分)求不等式 的正整数解.
的正整数解.
14.(本小题满分5分)解分式方程: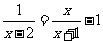 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com