
23.(6分)为保证交通安全,汽车驾驶员必须知道汽车刹车后的停止距离(开始刹车到车辆停止车辆行驶的距离)与汽车行驶速度(开始刹车时的速度)的关系,以便及时刹车.下表是某款车在平坦道路上, 路况良好时刹车后的停止距离与汽车行驶速度的对应值表:
|
行驶速度(千米/时) |
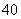 |
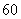 |
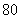 |
 |
|
停止距离(米) |
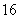 |
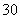 |
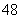 |
 |
(1)设汽车刹车后的停止距离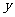 (米)是关于汽车行驶速度
(米)是关于汽车行驶速度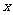 (千米/时)的函数,给出以下三个函数:①
(千米/时)的函数,给出以下三个函数:①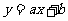 ;②
;②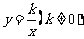 ;③
;③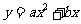 ,请选择恰当的函数来描述停止距离
,请选择恰当的函数来描述停止距离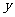 (米)与汽车行驶速度
(米)与汽车行驶速度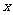 (千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;(2)如果汽车刹车后的停止距离为
(千米/时)的关系,说明选择理由,并求出符合要求的函数的解析式;(2)如果汽车刹车后的停止距离为 米,那么根据你所选择的函数解析式,求汽车的行驶速度.
米,那么根据你所选择的函数解析式,求汽车的行驶速度.
22.(5分)如图,梯形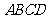 中,
中,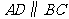 ,
,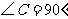 ,且
,且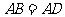 .联结
.联结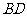 ,过点
,过点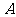 作
作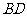 的垂线,交
的垂线,交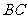 于点
于点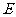 ,垂足为
,垂足为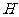 .如果
.如果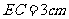 ,
,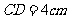 ,求梯形
,求梯形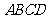 的面积.
的面积.
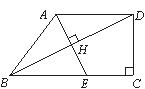
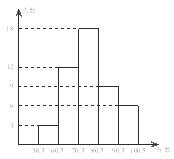
21.(6分)某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:(1)这个班有多少人参加了本次数学调研考试?(2)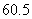 -
-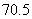 分数段的频数和频率各是多少?(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.
分数段的频数和频率各是多少?(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.
20.(5分)用两个全等的正方形 和
和 拼成一个矩形
拼成一个矩形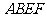 ,把一个足够大的直角三角尺的直角顶点与这个矩形的边
,把一个足够大的直角三角尺的直角顶点与这个矩形的边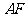 的中点
的中点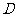 重合,且将直角三角尺绕点
重合,且将直角三角尺绕点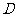 按逆时针方向旋转.
按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形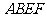 的两边
的两边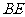 、
、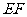 相交于点
相交于点 、
、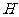 时,(如图甲),通过观察或测量
时,(如图甲),通过观察或测量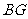 与
与 的长度,你能得到什么结论?并证明你的结论.
的长度,你能得到什么结论?并证明你的结论.
(2)当直角三角尺的两直角边分别与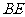 、
、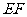 的延长线相交于点
的延长线相交于点 、
、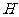 时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.
时(如图乙),你在图甲中得到的结论还成立吗?简要说明理由.

解:(1)得到的结论是 .
(2)得到的结论 .(填写“成立”、“不成立”)
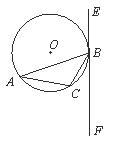
19.(5分)已知:△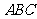 内接于⊙
内接于⊙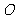 ,过点
,过点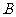 作直线
作直线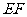 ,
,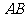 为非直径的弦,且
为非直径的弦,且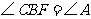 。(1)求证:
。(1)求证: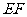 是⊙
是⊙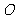 的切线;(2)若
的切线;(2)若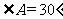 ,
,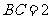 ,联结
,联结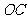 并延长交
并延长交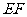 于点
于点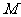 ,求由弧
,求由弧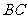 、线段
、线段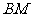 和
和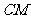 所围成的图形的面积.
所围成的图形的面积.
18.(本小题满分5分) 已知:关于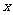 的一元二次方程
的一元二次方程 .求证:不论
.求证:不论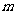 取何值时,方程总有两个不相等的实数根.
取何值时,方程总有两个不相等的实数根.
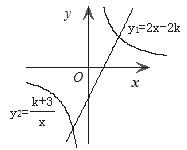
17.( 6分)已知一次函数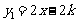 的图象与反比例函数
的图象与反比例函数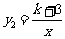 的图象相交,其中一个交点的纵坐标为-4.(1)求两个函数的解析式;(2)结合图象求出当
的图象相交,其中一个交点的纵坐标为-4.(1)求两个函数的解析式;(2)结合图象求出当 时,
时,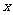 的取值范围.
的取值范围.
16.( 5分)为响应承办“绿色奥运”的号召,某班组织部分同学义务植树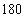 棵,由于同学们的积极参与,实际参加的人数比原计划增加了
棵,由于同学们的积极参与,实际参加的人数比原计划增加了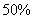 ,结果每人比原计划少栽了
,结果每人比原计划少栽了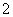 棵,问实际有多少人参加了这次植树活动?
棵,问实际有多少人参加了这次植树活动?
15.( 5分)先化简再求值: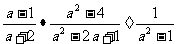 其中
其中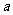 满足
满足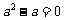 .
.
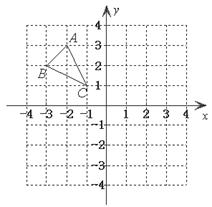
14.(4分)△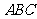 在平面直角坐标系中的位置如图所示,现将△
在平面直角坐标系中的位置如图所示,现将△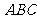 经过两次变换:第一次是作出△
经过两次变换:第一次是作出△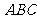 关于
关于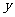 轴对称的△
轴对称的△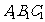 ;再将△
;再将△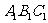 向下平移4个单位长度,得到△
向下平移4个单位长度,得到△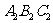 .请你在下面的网格中画出平移后的△
.请你在下面的网格中画出平移后的△ .(不写作法,保留作图痕迹,指明结果)
.(不写作法,保留作图痕迹,指明结果)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com