3. 已知△ABC的面积为36，将△ABC沿BC平移到△A´B´C´，使B′和C重合，连接AC′交A′C于D，则△C´DC的面积为(　　 )

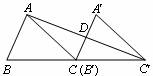
(A)6　　　　　　　　 (B)9　(C)12　　　　　　　　　　　　　　 (D)18

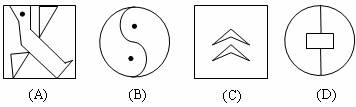
2. 下列图形中，是轴对称图形但不是中心对称图形的是(　)

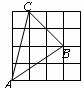
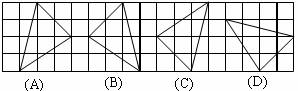
1、如图，在下面的四个三角形中，不能由△ABC经过旋转或平移得到的是(　)

28．(本小题满分10分)

(1)①已知如图1的△ABC中，∠A=60°,∠B=60°，请画一条直线，把这个三角形分割成两个三角形，其中一个三角形与原三角形相似，另一个三角形为等腰三角形．(在图中标出等腰三角形中相等两角的度数)

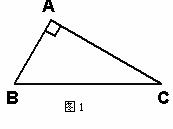
②如图2的△ABC中，∠A=110°∠B=40°，请画一条直线，把这个三角形分割成两个三角形，其中一个三角形与原三角形相似，另一个三角形为等腰三角形．(在图中标出等腰三角形中相等两角的度数)

(2)已知在△ABC中(∠B为最大角)，过顶点B的一条直线把这个三角形分割成了两个三角形，其中一个三角形与原三角形相似，另一个三角形为等腰三角形，请探求∠ABC与∠C之间的关系．

27．(本小题满分11分)

已知：如图，tan∠MON=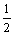，梯形ABCD在∠MON内部，且点A在OM上，BC在ON上，AB= 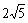cm，AD=1 cm，且tan∠ABC=2, tan∠DCB=4.点P从点O出发，以每秒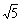cm的速度在射线OM上匀速运动，点Q、R在射线ON上，且PQ∥AB，PR⊥ON于R.设点P运动了x秒.

(1)用x表示线段PR的长为　　　　　　 cm；

(2)当x=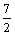时，△PQR与梯形ABCD重叠部分的面积S=　　　　　　 ；

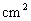　　 当x=5时，△PQR与梯形ABCD重叠部分的面积S=　　　　　　 ；

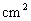(3)当4≤x≤5时，求△PQR与梯形ABCD重叠部分的面积S与x的函数关系式.

26．(本小题满分8分)

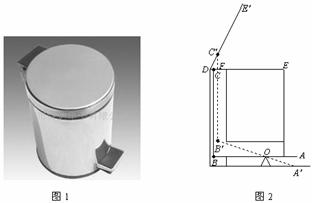
如图1是脚踏式垃圾桶，图2是它的内部结构示意图.当用脚将点A踩至地面点A′处时，水平横杆AB、竖杆BC就借助支点O和活动轴心(点B、点C)移到A′B′、B′C′位置，并将水平桶盖DE顶至DE′位置，即桶盖被打开.图中DE⊥B′C′，垂足为点F,设计要求是∠C′DF至少为75°.已知AO=8.5cm，OB=17cm，竖杆BC与垃圾桶左侧外壁之间的距离DC=0.48cm，水平横杆AB到地面的距离为1.3cm.问：这个脚踩式垃圾桶符合设计要求吗？请说明理由.

25．(本小题满分8分)

2008年8月24日将在北京奥林匹克篮球馆举行男子篮球冠亚军决赛，某校准备组织50名师生前往观看.已知当天门票价格如表所示：

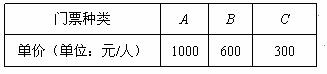
要求：① B类门票的张数和C类门票的张数相等；② 每类门票都必须购买。

(1)学校最多要准备　　　　　　　　 元的门票费用.

(2)由于学校经费紧张，经预算：门票总费用不低于22000元，但又不超过25000元，请分析有几种购买门票的方式？并列举出来.

24．(本小题满分6分)

(1)比较大小：

① 3+5　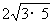　 ；　　 ② 　　　；

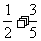
③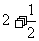　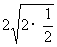 ；　　 ④ 6+6　　 .

(2)通过(1)的判断，你可猜想：

当a、b为正实数时，与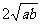的大小关系为　　　 .

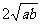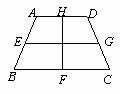
(3)利用上述猜想解决下列问题：如图，有一等腰梯形的工件(厚度不计)，其面积为1800cm²，现要用包装带如图包扎(四点为四边中点)，则最少需要包装带的长为　　　 cm.

23．(本小题满分7分)

数学老师将本班学生的身高数据(精确到l厘米)交给甲、乙两同学，要求他们各自独立地绘制一幅频数分布直方图．甲绘制的如图1所示，乙绘制的如图2所示，经确认，甲绘制的图是正确的，乙在整理数据与绘图过程中均有个别错误．

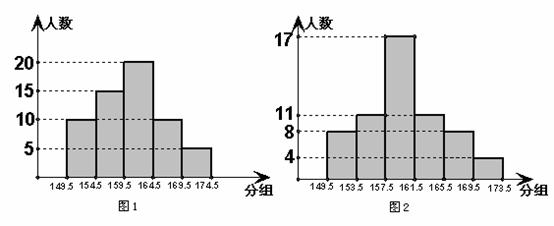
请回答下列问题：

(1)该班学生有多少人?

　(2)甲同学身高为165厘米，他说：“我们班上比我高的人不超过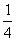”．他的说法正确吗?说明理由．

　　 (3)写出乙同学在整理或绘图过程中的错误(写出一个即可)．

22．(本小题满分8分)

4月8日，无锡迎来了第二个“城市旅游日”， 全市各大公园将向市民特惠开放。下表是小华和小明姐弟俩选择的感兴趣的四个景区及特惠门票的价格。为了开阔眼界，他们决定两人去不同的景区。他们制作了两个质地均匀的正四面体骰子，上面分别标着四个景区名称，他们两人各抛掷一枚正四面体骰子，着地的那个面就表示要去旅游的景区.(如果得到相同的景区，规定重新抛掷)

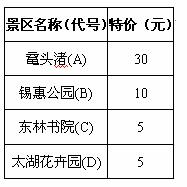
(1)他们去游玩的景区组合共有几种？

(2)他们两人旅游的门票总费用不超过35元的概率是多少？ 请写出分析过程.