4．解集在数轴上表示为如图所示的不等式组是　　 (　　 )

A．　 　 B．　 　　　　　　 C．　　　　 D．

3．随机掷两枚硬币，落地后全部正面朝上的概率是　　 (　　 )

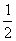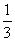　　 A．1　　 　　　　　　　 B．　　　　　　　　　 C．　　 　　　　　　 D．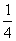

2．第九届海峡交易会5月18日在榕城开幕，推出的重点招商项目总投资约450亿元人民币，将450亿元用科学记数法表示为　 (　　 )

　　 A．0.45×10¹¹元　　 B．4.50×10⁹元　 　 C．4.50×10¹⁰元　　　　　　 D．450×10⁸元

1．在平面直角坐标系中，点(3，一4)所在的象限是　　 (　　 )

　　 A．第一象限 　　　 B．第二象限　　 　 C．第三象限　　　　 D．第四象限

28．(本题13分)如图21，在平面直角坐标系中，已知点A(0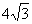，)，点B在z正半轴上，且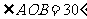．动点P在线段AB上从点A向点8以每秒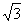个单位的速度运动，设运动时间为秒．在z轴上取两点M， N作等边△PMN．

(1)求直线AB的解析式．

(2)求等边△PMN的边长(用t的代数式表示)，并求出当等边△PMN的顶点M运动到与原点。重合时t的值．

(3)如果取OB的中点D，以0D为边在Rt△A()B内部作如图22所示的矩形ODCE，点C在线段AB上．设等边△PMN和矩形ODCE重叠部分的面积为S，请求出当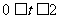秒时S与的函数关系式，并求出S的最大值。

27．(本题10分)在图16-20中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边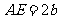，且边AD和AE在同一直线上．

操作示例：当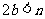时，如图16，在BA上选取点G，使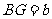，连接FG和CG，裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．

思考发现：小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90º到△FEH的位置，易知EH与AD在同一直线上．连接CH，由剪拼方法可得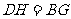，故△CHD ≌△CGB，从而又可将△CGB绕点C顺时针旋转90º到△CHD的位置．这样，对于剪拼得到的四边形FGCH(如图16)，过点F作FM上AE于点M(图略)，利用SAS公理可判断△HFM≌△CHD，易得FH＝HC＝GC＝FG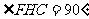，．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．

实践探究：

(1)正方形FGCH的面积是　　　　　　　　　　 ；(用含a，b的式子表示)

(2)类比图16的剪拼方法，请你就图17一图19的三种情形分别画出剪拼成一个新正方形的示意图．

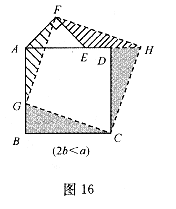
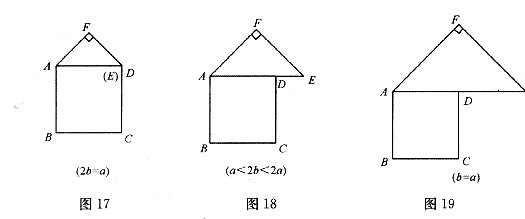
联想拓展：小明通过探究后发现：当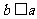时，此类图形者能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．当时，如图20的图形能否剪拼成一个正方形？若能请你在图中画出剪拼的示意图；若不能，简要说明理由．

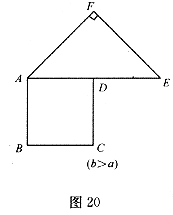
26．(本题l2分)某校九年级三班为开展“迎2008年北京奥运会”的主题班会活动，派了小林和小明两位同学去学校附近的超市购买钢笔作为奖品．已知该超市的锦江牌钢笔每支8元，红梅牌钢笔每支4.8元，他们要购买这两种笔共40支．

(1)如果他们两人一共带了240元，全部用于购买奖品，那么能买这两种笔各多少支?

(2)小林和小明根据主题班会活动的设奖情况，决定所购买的锦江牌钢笔的数量要少于红梅牌钢笔的数量的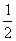，但又不少于红梅牌钢笔的数量的．如果他们买了锦江牌钢笔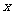支，买这两种笔共花了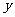元．

①请写出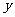(元)关于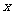(支)的函数关系式，并求出自变量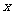的取值范围．

②请帮他们计算一下，这两种笔各购买多少支时，所花的钱最少，此时花了多少元?

25．(本题10分)在课外活动时间，小王、小丽、小华做“互相踢踺子”游戏，踺子从一人传到另一人就记为踢一次．

(1)若从小丽开始，经过两次踢踺后，踺子踢到小华处的概率是多少?(用树状图或列表法说明)

(2)若经过三次踢踺后，踺子踢到小王处的可能性最小，应确定从谁开始踢，并说明理由．

24．(本题满分10分)如图14，在平面直角坐标系中，以坐标原点O为圆心，2为半径画⊙O，P是⊙O上一动点，且P在第一象限内，过点P作⊙O的切线与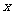轴相交于点A，与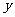轴相交于点B．

(1)点P在运动时，线段AB的长度也在发生变化，请写出线段AB长度的最小值，并说明理由．

(2)在⊙O上是否存在一点Q，使得以Q，O，A，P为顶点的四边形是平行四边形？若存在，请求出Q点的坐标；若不存在，请说明理由．

23．(本题8分)小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：

方法一：选择合适的一种方法(公式法、配方法、分解因式法)求解

　　 解方程：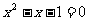

　　 解：

方法二：利用二次函数图像与坐标轴的交点求解如图13所示，把方程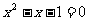的解看成是二次函数　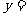 　　　　　　　 　　　 的图像与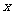轴交点的横坐标，即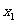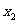，就是方程的解．

方法三：利用两个函数图像的交点求解

(1)把方程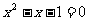的解看成是一个二次函数　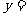　　　　　　　　 的图像与一个一次函数　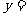　　　　　　　　　 图像交点的横坐标；

(2)画出这两个函数的图像，用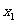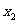，在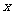轴上标出方程的解．