26．(本小题满分12分)

如图12a，点C将线段AB分成两部分，如果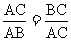，那么称点C为线段AB的黄金分割点。

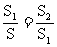某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线将一个面积为S的图形分成两部分，这两部分的面积分别为S₁，S₂，如果，那么称直线为该图形的黄金分割线。

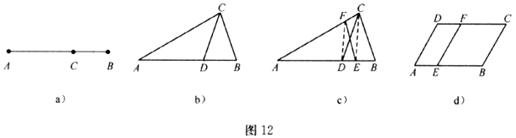
(1)研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点(如图12b)，则直线CD是△ABC的黄金分割线，你认为对吗？为什么？

(2)请你说明：三角形的中线是否也是该三角形的黄金分割线？

(3)研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF(如图12c)，则直线EF也是△ABC的黄金分割线。请你说明理由。

(4)如图12d，点E是□ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是□ABCD的黄金分割线。请你画一条□ABCD的黄金分割线，使它不经过□　ABCD各边黄金分割点。

25．(本题满分11分)

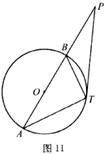
如图11，⊙O的直径AB的延长线交TP于P，若PA=18，PT=12，PB=8。

(1)求证：△PTB ∽△PAT。

(2)求证：PT为⊙O的切线。

24．(本题10分)

小军与小玲共同发明了一种“字母棋”，进行比胜负的游戏．她们用四种字母做成10只棋子，其中A棋1只，B棋2只，C棋3只，D棋4只。

“字母棋”的游戏规则为：

①游戏时两人各摸一只棋进行比赛称一轮比赛，先摸者摸出的棋不放回；

②A棋胜B棋、C棋；B棋胜C棋、D棋；C棋胜D棋；D棋胜A棋；

③相同棋子不分胜负。

(1)若小玲先摸，问小玲摸到C棋的概率是多少？

(2)已知小玲先摸到了C棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲胜小军的概率是多少？

(3)已知小玲先摸一只棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲希望摸到哪种棋胜小军的概率最大？

23．(本题满分7分)

如图9所示为某次国际马拉松赛中半程马拉松、10km赛程、5km赛程各项目参赛人数占全体参赛人数比例的扇形统计图。

(1)求参加全程马拉松赛的人数占全体参赛人数的百分比。

(2)已知参加10m赛程的人数为7200人，求参加全程马拉松赛的人数。

22．(本题8分)

如图8，不透明圆锥体DEC放在水平面上，在A处灯光照射下形成影子。设BP过底面圆的圆心，已知圆锥体的高为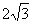m，底面半径为2m，BE=4m。

(1)求∠B的度数。

(2)若∠ACP=2∠B，求光源A距水平面的高度(答案用含根号的式子表示)。

21．(本题满分7分)

先化简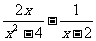：，然后请你自选一个合理的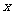值，求原式的值。

20．(本题满分7分)解方程：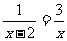

19．(本题满分6分)计算：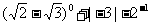

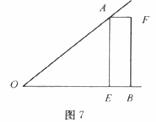
18．如图7，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是矩形。请你只用无刻度的直尺在图中画出∠AOB的平分线(请保留画图痕迹)。

17．如图6，左右两条抛物线关于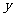轴对称，左边的抛物线是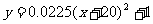，则右边的抛物线是　　　　　　 。