
6.等腰三角形一腰上的离与另一腰的夹角为30°,则顶角度数为( )
A.60° B.120° C.60°或l50°D.60°或l20°
5.若规定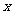 ※y=3
※y=3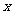 一2y+1,则(一2)※(3※4)的值为( )
一2y+1,则(一2)※(3※4)的值为( )
A.8 B.一8 C.9 D.一9
4.若5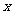 2ym与4xn+m-1y的和是单项式,则代数式m2一n的值是( )
2ym与4xn+m-1y的和是单项式,则代数式m2一n的值是( )
A.1 B.一l C.一3 D.3
3.为了了解八年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算仰卧起坐次数在l5-20次之间的频率是( )
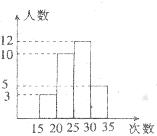
A.0.1 B.0.17 C.0.33 D.0.4
2.下列等式从左到右的变形是正确的因式分解的是( )
A.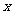 2y+
2y+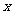 =
=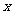 2(y+
2(y+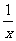 ) B.
) B.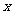 2一
2一
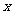 -
-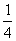 =(
=(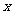 一
一 )2
)2
C.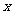 4一y4=(
4一y4=(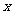 2+y2)(
2+y2)(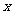 +y)(
+y)(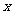 -y) D.一
-y) D.一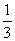 a一9a4=-a(
a一9a4=-a(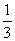 -9a3)
-9a3)
1.下面是某同学在一次测验中的计算摘录:( )
①6a+2b=8ab ②4m3n一5mn3=-m3n ③3x2·(一2x3)=-6x5 ④14a3b÷(一7a2b)=-2a ⑤(a3)3=a6 ⑥(一a)3÷(一a)=-a2,其中正确的个数有
A.1个 B.2个 C.3个 D.4个
25.(本题满分8分)
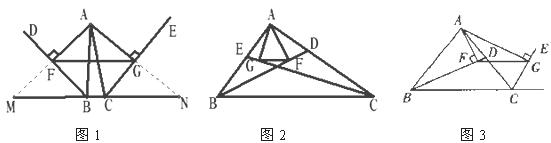
(1)如图10-1所示,BD, CE分别是△ABC的外角平分线,过点A作AF⊥BD, AG⊥CE,垂足分别为F,G,连结FG,延长AF, AG,与直线BC分别交于点M、N,那么线段FG与△ABC的周长之间存在的数量关系是什么?即:FG= (AB+BC+AC) (直接写出结果即可)
(2)如图10-2,若BD,CE分别是△ABC的内角平分线;其他条件不变,线段FG与
ΔABC三边之间又有怎样的数量关系?请写出你的猜想,并给予证明.
(3)如图10-3,若BD为△ABC的内角平分线,CE为△ABC的外角平分线,其他条件不变,线段FG与ΔABC三边又有怎样的数量关系?直接写出你的猜想即可.不需要证明。
答:线段FG与ΔABC三边之间数量关系是 。
24.已知:抛物线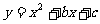 的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C,
的对称轴是x=2,且经过点A(1,0),且与x轴的另一个交点为B,与y轴交于点C,
(1)确定此二次函数的解析式及顶点D的坐标;
(2)将直线CD沿y轴向下平移3个单位长度,求平移后直线m的解析式.
(3)在直线m上是否存在一点E,使得以点E、A、B、C为顶点的四边形是梯形,如果存在,求出满足条件的E点的坐标,如果不存在,说明理由。
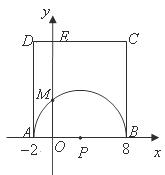
23. 如图,在平面直角坐标系中,A,B两点的坐标分别为A(-2,0),B(8,0),以AB为直径的半圆P与y轴交于点M,以AB为一边作正方形ABCD.
(1)求C,M两点的坐标;
(2)试判断直线CM与半圆P的位置关系,并证明你的结论。
(3)在x轴上是否存在一点Q,使得△QMC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
22. 在△ABC中,AB=AC,∠A=36°,把像这样的三角形叫做黄金三角形。
(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,联结 EF并延长交 BC的延长线于M。试判断CM与AB之间的数量关系?只需说明结果,不用证明。
答:CM与AB之间的数量关系是 。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com