
3.若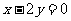 ,则
,则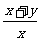 的值是
的值是
A.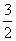 B.
B.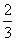 C.
C.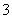 D.
D.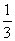
2.下列各式中与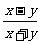 相等的是
相等的是
A. B.
B.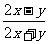 C.
C.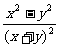 D.
D.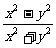
1.当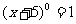 时,则
时,则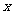 的取值范围是
的取值范围是
A. B.
B. C.
C.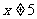 D.
D.
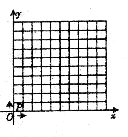
25.(12分)如图,在平面直角坐标系中,横、纵坐标都为整数的点叫做整点。设坐标轴的单位长为1厘米,整点P从原点O出发:速度为1厘米/秒,且点P只能向上或向右运动。 请回答下列问题:
(1)填表:
|
P从O点出发 的时间 |
可得到的整点的坐标 |
可以得到的 整点的个数 |
|
1秒 |
(0,1)、(1,0) |
2个 |
|
2秒 |
|
|
|
3秒 |
|
|
(2)当点P从点O出发4秒时,可能得到的整点的坐标是 ;
(3)当点P从点O出发10秒时,可得到的整点个数是 个;
(4)当点P从O点出发 秒时,可得到整点(10,5);
(5)当点P从点O出发30秒时,整点P恰好在直线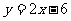 上,求P点坐标。
上,求P点坐标。
(6)若设点P从点O出发的时间为t(秒)时,试与出n与t之间的函数关系式,并写出t的取值范围。
24.(12分)某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成下图,请根据图象回答:
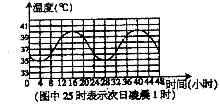
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多长时间?
(2)第三天12时这头骆驼的体温是多少?
(3)兴趣小组又在研究中发现,图中10时到22时的曲线是抛物线,求该抛物线的关系式。
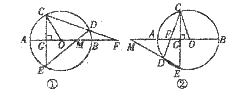
23.(12分)(1)如图①,⊙O的弦CE垂直于直径AB,垂足为点G,点D在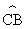 上,作直线CD、ED与直线AB分别交于点F,M,连接OC。求证:OC2=GM·OF;
上,作直线CD、ED与直线AB分别交于点F,M,连接OC。求证:OC2=GM·OF;
(2)把(1)中的“点D在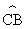 上”改为“点D在
上”改为“点D在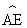 上”,其余条件不变(如图②),试问:(1)中的结论是否成立?并说明理由。
上”,其余条件不变(如图②),试问:(1)中的结论是否成立?并说明理由。
22.(12分)如图所示,已知某小区的两幢10层住宅楼间的距离为AC=30m。由地面向上依次为第1层、第2层、…、第10层,每层高度为3m,假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为 。
。
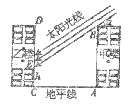
(1)用含 的式子表示h;(不必指出
的式子表示h;(不必指出 的取值范围)
的取值范围)
(2)当 =30º时,甲楼楼顶B点的影子落在乙楼的第几层?若
=30º时,甲楼楼顶B点的影子落在乙楼的第几层?若 每小时增加15º,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
每小时增加15º,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
21.(8分)四张质地相同的卡片如图所示,将卡片洗匀后,背面朝上放置在桌面上。
(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则如信息图。你认为这个游戏公平吗?请用列表法或画树状图法说明理由,若认为不公平,请你修改规则,使游戏变得公平。

20.(8分)为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容,为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容)。整理调查结果,绘制统计图如下:

请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为 名;
(2)该校有300名学生,估计喜欢收听易中天《品三国》的学生有 名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的 %;
(4)你认为上述估计合理吗?理由是什么?
19.(8分)如图,在Rt△ABC中,∠C=90。,BC=1,AC=2,把边长分别为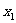 、
、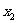 、
、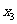 …
…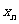 的n个正方形依次放入△ABC中,请回答下列问题:
的n个正方形依次放入△ABC中,请回答下列问题:
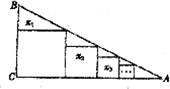
(1)按要求填表:
|
n |
1 |
2 |
3 |
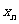 |
|
|
|
(2)第n个正方形的边长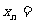 ;
;
(3)若m、n、p、q是正整数,且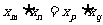 ,试判断m、n、p、q的关系。
,试判断m、n、p、q的关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com