

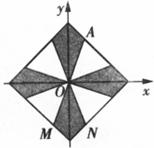
6.如上右图所示,有一张一个角为60°的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是
A.邻边不等的矩形 B.等腰梯形
C.有一角是锐角的菱形 D.正方形
5.如下左图,阴影部分组成的图案既是关于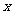 轴成轴对称的图形,又是关于坐标原点O成中心对称的图形。若点A的坐标是(1,3),则点M和点N的坐标分别为
轴成轴对称的图形,又是关于坐标原点O成中心对称的图形。若点A的坐标是(1,3),则点M和点N的坐标分别为
A.M(1,-3),N(-1,-3) B.M(-1,-3),N(-1,3)
C.M(-1,-3),N(1,-3) D.M(-1,3),N(1,-3)
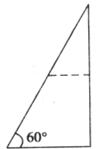
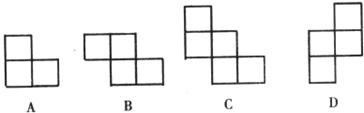
4.如图甲是一些大小相同的小正方体组成的几何体,其主视图如图乙所示,则其俯视图是
3.不等式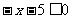 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是

2.为支援四川地震灾区,中央电视台于5月18日晚举办了《爱的奉献》赈灾晚会,晚会现场捐款达1514000000元。1514000000用科学记数法表示正确的是
A.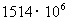 B.
B.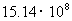 C.
C.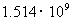 D.
D.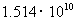
1.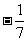 的绝对值是
的绝对值是
A.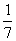 B.
B. C.7 D.-7
C.7 D.-7
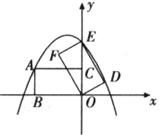
26.如下图所示,在平面直角坐标系中,矩形ABOC的边BO在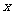 轴的负半轴上,边OC在
轴的负半轴上,边OC在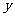 轴的正半轴上,且AB=1,OB=
轴的正半轴上,且AB=1,OB=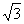 ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD。点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD。点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线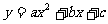 过点A、E、D。
过点A、E、D。
(1)判断点E是否在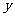 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在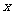 轴的上方是否存在点P、点Q,使以点O、B、P、Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上,若存在,请求出点P、点Q的坐标;若不存在,请说明理由。
轴的上方是否存在点P、点Q,使以点O、B、P、Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上,若存在,请求出点P、点Q的坐标;若不存在,请说明理由。
25.已知:如下图甲所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B、A、D在一条直线上,连结BE、CD,M、N分别为BE、CD的中点。
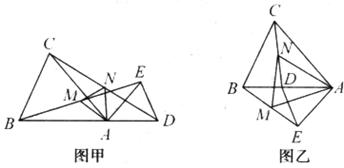
(1)求证:①BE=CD;②△AMN是等腰三角形。
(2)在图甲的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图乙所示的图形。请直接写出(1)中的两个结论是否仍然成立;
(3)在(2)的条件下,请你在图乙中延长ED交线段BC于点P。求证:△PBD∽△AMN。
24.一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往与A处相距636千米的B地,下表记录的是货车一次加满油后油箱内余油量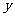 (升)与行驶时间
(升)与行驶时间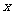 (时)之间的关系:
(时)之间的关系:
行驶时间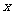 (时) (时) |
0 |
1 |
2 |
2.5 |
余油量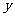 (升) (升) |
100 |
80 |
60 |
50 |
(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示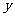 与
与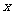 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从A处出发行驶4.2小时到达C处,求此时油箱内余油多少升?
(3)在(2)的前提下,C处前方18千米的D处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B地。(货车在D处加油过程中的时间和路程忽略不计)
23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
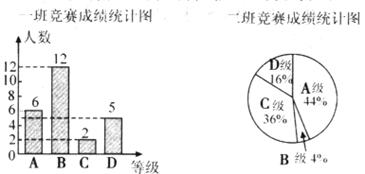
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为 ;
(2)请你将表格补充完整:
|
|
平均数(分) |
中位数(分) |
众数(分) |
|
一班 |
87.6 |
90 |
|
|
二班 |
87.6 |
|
100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行分析:
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com