5．已知Rt△ABC的斜边AB=13cm，一条直角边AC=5cm，以直线BC为轴旋转一周得一个圆锥，则这个圆锥的表面积是(　 　)cm²。

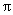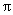A．65　　 　　　　　　　　 B．90　　 　　　　　　　　 C．156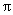　　　　　　　　　　 D．300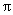

4．在同一直角坐标系中，一次函数与二次函数的图像大致为(　 　)

3．期中考试后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M∶N为(　 　)

A．40／41　　 　　　　　　 B．1 　　　　　　　　　　　　 C．41／40　　 　　　　　　 D．2

2．半径为7的圆，其圆心在坐标原点，则下列各点在圆外的是：(　 　)

A．(3，4)　　 　　　　 B．(4，4)　　 　　　　 C．(4，5)　　　　　　　 D．(4，6)

1．若关于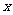的方程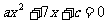的两根均为正数，则点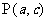在第(　 　)象限。

A．一　　 　　　　　　　　　 B．二　　 　　　　　　　　　 C．三　　 　　　　　　　　　 D．　 四

24．(本题满分12分)

　 如图，在平面直角坐标系中，坐标原点为O，A点坐标为(4，0)，B点坐标为(-1，0)，以AB的中点P为圆心，AB为直径作圆P与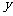轴的正半轴交于点C．

　　 (1)求经过A、B、C三点的抛物线对应的函数表达式；

　　 (2)设M为(1)中抛物线的顶点，求直线MC对应的函数表达式；

　　 (3)试说明直线MC与圆P的位置关系，并证明你的结论．

23．(本题满分11分)

　　 某农户计划利用现有的一面墙再修四面墙，建造如图所示的长方体水池，培育不同品种的鱼苗．他已备足可以修高为1.5m、长18m的墙的材料准备施工，设图中与现有一面墙垂直的三面墙的长度都为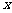m，即AD=EF=BC=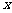m．(不考虑墙的厚度)

　　 (1)若想水池的总容积为36m³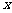，应等于多少？

　　 (2)求水池的总容积V与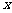的函数关系式，并直接写出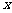的取值范围；

　　 (3)若想使水池的总容积V最大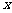，应为多少?最大容积是多少?

22．(本题满分10分)

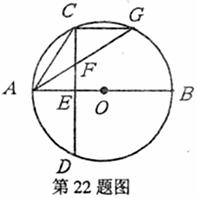
　　 如图，己知AB是圆O的直径，弦CD上AB于E，F是CE上的一点，且FC=FA，延长AF交圆O于G，连结CG．

　　 (1)试判断△ACG的形状(按边分类)，并证明你的结论；

　　 (2)若圆O的半径为5，OE=2，求CF·CD的值．

21．(本题满分10分)

　　 O点是△ABC所在平面内一动点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，如果DEFG能构成四边形．

　　 (1)如图，当D点在△ABC内时，求证四边形DEFG是平行四边形；

　　 (2)当O点移动到△ABC外时，(1)的结论是否成立?画出图形并说明理由；

　　 (3)若四边形DEFG为矩形，O点所在位置应满足什么条件?试说明理由．

20．(本题满分10分)

　 某班到毕业时共结余班费1800元，班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品，其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品．己知每件文化衫比每本相册贵9元，用200元恰好可以买到2件文化衫和5本相册．

　 (1)求每件文化衫和每本相册的价格分别为多少元?

　 (2)有几种购买文化衫和相册的方案?哪种方案用于购买老师纪念品的资金更充足?