
4.在统计中,样本的方差可以近似地反映总体的
A.平均状态 B.波动大小 C.分布规律 D.集中趋势
3.一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为
A.10米 B.15米 C.25米 D.30米
2.已知正比例函数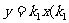 ≠0)与反比例函数
≠0)与反比例函数 ≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是
≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是
A.(2,1) B.(-2,-l) C.(-2,1) D.(2,-l)
1.下列各式中,分式的个数有
 、
、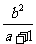 、
、 、
、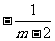 、
、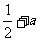 、
、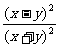 、
、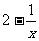 、
、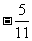
A.2个 B.3个 C.4个 D.5个
(21)如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,有下面4个结论:

①BD是∠ABC的角平分线;②△BCD是等腰三角形:③△ABC∽△BCD;④△MBD∽△BCD。
(1)判断其中正确的结论是哪几个;(4分)
(2)从你认为是正确的结论中选一个加以证明。(6分)
(22)解下列方程(每题4分共8分)
①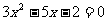 ②7
②7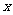 (
(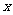 一3)=4(3一
一3)=4(3一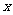 )
)
(23)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫降价2元,商场平均每天可多售出4件。若商场平均每天销售这种衬衫的盈利要达到1200元,每件衬衫应降价多少元?(6分)
(24)如图所示,已知A、B两点的坐标分别为(28,0)和(0,28),动点P从A点开始在线段AO上以每秒3个单位长度的速度向原点O运动,动直线EF从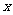 轴开始以每秒1个单位长度的速度向上平移(即EF//
轴开始以每秒1个单位长度的速度向上平移(即EF//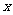 轴),并且EF分别与y轴、线段AB交于E、F点,连接FP,设动点P与动直线EF同时出发,运动时间为t秒,求当梯形OPFE的面积等于△APF的面积时线段PF的长。(6分)
轴),并且EF分别与y轴、线段AB交于E、F点,连接FP,设动点P与动直线EF同时出发,运动时间为t秒,求当梯形OPFE的面积等于△APF的面积时线段PF的长。(6分)
(25)如图,电线杆上有一盏路灯O,电线杆与三个等高的标杆整齐地排列在马路一侧的直线上,AB、CD、EF是三个标杆,相邻的两个标杆之间的距离都是2m,己知AB、CD在灯光下的影长分别为BM=16m,DN=0.6m.
(1)请画出路灯O的位置和标杆EF在路灯光下的影子。(4分)
(2)求标杆EF的影长。(6分)

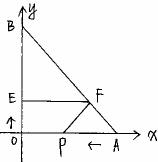
(11)如图,AB=AC,EB=EC,AE的延长线交BC于点D,那么图中的全等三角形共有_______对。
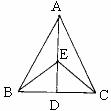
(12)如图,点角三角形ABC中,∠A=90°,AB=3cm,AC=4cm,以斜边上距离点B 3cm的点P为中心把这个三角形逆时针方向旋转90°,得到△DEF,则旋转前后的两个三角形重叠部分的面积为_______cm2。
(13)已知|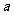 |=3,且
|=3,且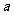 +|
+|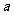 |=0,则
|=0,则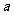 3+
3+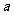 2+
2+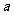 +l=_______。
+l=_______。
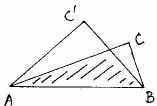
(14)如图,一副三角板叠在一起,若∠C’AB=45°∠CAB=30°,AB=6,则阴影部分的面积为_______。
(15)已知:平行四边形ABCD中,AB=12,AB边上的高为3,BC边上的高为6,则平行四边形ABCD的周长为______________。
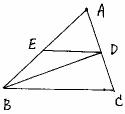
(16)已知:如图,△ABC中,BD平分∠ABC,且D为AC的中点,DE//BC交AB于点E,若BC=4,则EB长为 ______________。
(17)已知一元二次方程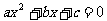 ,若
,若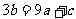 ,则此方程必有一个解为_______。
,则此方程必有一个解为_______。
(18)有一反比例函数在它的图像上有一点M,由M向两个坐标轴作垂线,两垂线与两坐标轴转成的小矩形面积为6,则此反比例函数的解析式为_______________________。
(19)反比例函数y=k/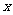 与一次函数y=k
与一次函数y=k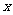 +m的图像有一个交点是(-2,1),则它们的另一个交点的坐标为______________。
+m的图像有一个交点是(-2,1),则它们的另一个交点的坐标为______________。
(20)如果一元一次方程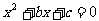 的两个根为-2,1,那么字母
的两个根为-2,1,那么字母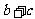 =__________。
=__________。
(1)对于任意三角形,下列各点:
①三条中线的交点;②三条角平分线的交点;③三条高的交点;④三边垂直平分线的交点。
其中一定在三角形内部的有 ( )
A、1个 B、2个 C、3个 D、4个
(2)如图,四边形ABCD的对角线AC、BD相交于点O,如果△BOC的面积为3,△AOD的面积为4,△BOA的面积为5,那么△DOC的面积为 ( )
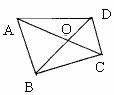
A、2 B、2.4 C、2.5 D、2.6
(3)给出下面四个命题:①有一组对边平行的四边形是梯形:②一条对角线平分一个内角的平行四边形是菱形;③两条对角线互相垂直的矩形是正方形:④一组对边平行,另一组对边相等的四边形是平行四边形。其中真命题的个数有 ( )
A、1个 B、2个 C、3个 D、4个
(4)已知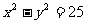 ,
,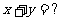 ,且
,且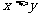 ,则
,则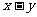 的值为 ( )
的值为 ( )
A、4 B、5 C、l D、1或一l
(5)商店某种货物的进价下降了8%,但售价不变,于是这种货物的销售利润由原来的a%增加到(a+10)%,则a的值为 ( )
A、8 B、10 C、15 D、20
(6)已知菱形ABCD的对角线的比为1: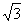 ,若AB=2,则菱形ABCD的面积为 ( )
,若AB=2,则菱形ABCD的面积为 ( )
A、2 B、2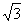 C、4
D、4
C、4
D、4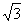
(7)如图,△ABC的三条中线相交于点O,若△ABE的面积为l8,则四边形CDOE的面积为 ( )
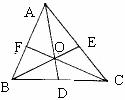
A、l2 B、15 C、9 D、无法确定
(8)面积为2的△ABC的一边长为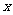 ,这个边上的高为y,则y与
,这个边上的高为y,则y与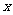 的变化规律用图像表示大致为下图中的 ( )
的变化规律用图像表示大致为下图中的 ( )

A B C D
(9)在同一坐标系中,函数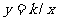 和
和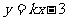 的图像大致是 ( )
的图像大致是 ( )

A B C D
(10)若点(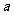 ,m)、(b,n)、(c,p)都是反比例函数y=-5/
,m)、(b,n)、(c,p)都是反比例函数y=-5/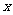 的图像上的点,并且
的图像上的点,并且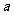 <0<b<c,则
<0<b<c,则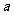 、n、p的大小关系为 ( )
、n、p的大小关系为 ( )
A、m<n<p B、m<p<n C、p<n<m D、n<p<m
23,已知抛物线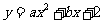 与
与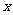 轴相交于点
轴相交于点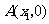 ,
,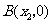
 ,且
,且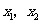 是方程
是方程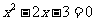 的两个实数根,点
的两个实数根,点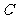 为抛物线与
为抛物线与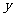 轴的交点.
轴的交点.
(1)求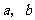 的值;
的值;
(2)分别求出直线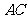 和
和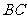 的解析式;
的解析式;
(3)若动直线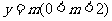 与线段
与线段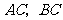 分别相交于
分别相交于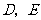 两点,则在
两点,则在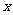 轴上是否存在点
轴上是否存在点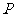 ,使得
,使得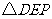 是等腰直角三角形?若存在,求出点
是等腰直角三角形?若存在,求出点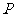 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
22,操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图18,19,20是旋转三角板得到的图形中的3种情况.
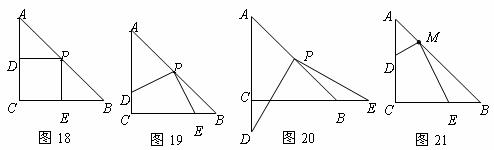
探究:(1)三角板绕点P旋转,通过观察或测量,猜想线段PD和PE之间有什么数量关系?并结合图19加以证明.
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,写出△PBE的腰长;若不能,请说明理由.
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图21加以证明.
21,如图17是按一定规律排列的方程组集合和它解的集合的对应关系图,若方程组处左至右依次记作方程组1、方程组2、方程组3、……方程组n.
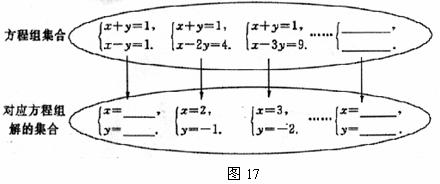
(1)将方程组1的解填入图中;
(2)请依据方程组和它的解变化的规律,将方程组n和它的解直接填入集合图中;
(3)若方程组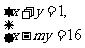 的解是
的解是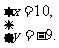 求m的值,并判断该方程组是否符合(2)中的规律?
求m的值,并判断该方程组是否符合(2)中的规律?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com