
3.如图,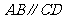 ,直线
,直线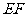 与
与 、
、 分别相交于
分别相交于 、
、 .
.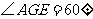 则
则 的度数是( )
的度数是( )

A.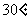 B.
B. C.
C. D.
D.
2.图中几何体的主视图是( )


1. 的相反数是(
)
的相反数是(
)
A.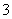 B.
B. C.
C. D.
D.
26.(本小题满分13分)
已知抛物线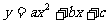 的图像交
的图像交 轴于点A(
轴于点A( ,0)和点B(2,0),与
,0)和点B(2,0),与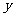 轴的正半轴交于点C,其对称轴是直线
轴的正半轴交于点C,其对称轴是直线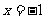 ,
, ,点A关于
,点A关于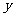 轴的对称点为点D。
轴的对称点为点D。
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于 轴的直线与(2)小题中所求抛物线交于M、N两点,以MN 为一边,抛物线上任一点P(
轴的直线与(2)小题中所求抛物线交于M、N两点,以MN 为一边,抛物线上任一点P( )为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标
)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标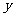 的函数解析式;
的函数解析式;
(4)当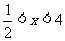 时,(3)小题中平行四边形的面积是否有最大值,若有,请求出;若无,请说明理由。
时,(3)小题中平行四边形的面积是否有最大值,若有,请求出;若无,请说明理由。
25.(本小题满分11分)
如下图(1),△ABC的边BC在直线 上,AC⊥BC,且AC=BC;△EFD的边FP也在直线
上,AC⊥BC,且AC=BC;△EFD的边FP也在直线 上,边EF与边AC重合,且EF=FD。
上,边EF与边AC重合,且EF=FD。

(1)如图(1)中,请你通过观察测量,猜想并写出AB与AP所满足的数量关系的位置关系;
(2)将△EFP沿直线 向左平移到图(2)的位置时,EP交AC于点Q,连结AP,BQ。猜想并写出BQ和AP所满足的数量关系和位置关系,请证明你的猜想;
向左平移到图(2)的位置时,EP交AC于点Q,连结AP,BQ。猜想并写出BQ和AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线 向左平移到图(3)的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ。你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
向左平移到图(3)的位置时,EP的延长线交AC的延长线于点Q,连结AP,BQ。你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。
24.(本小题满分10分)
在“5·12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000m2和乙种板材12000m2的任务。
(1)已知该企业安排140人生产这两种板材,每人每天能生产甲板材30m2或乙种板材20cm2,问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?
(2)某灾民安置点计划用该企业生产的这批板材搭建A、B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材,已知建一间A型板房和一问B型板房所需板材及能安置的人数如下表所示:
|
板房型号 |
甲种板材 |
乙种板材 |
安置人数 |
|
A型板房 |
54 m2 |
26 m2 |
5 |
|
B型板房 |
78 m2 |
41 m2 |
8 |
问:这400间板房最多能安置多少灾民?
23.(本小题满分9分)
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q 到达点C时,P、Q两点都停止运动。设运动时间 (s),解答下列问题:
(s),解答下列问题:

(1)当 时,判断BPQ的形状,并说明理由;
时,判断BPQ的形状,并说明理由;
(2)设△BPQ的面积为 (cm2),求
(cm2),求 与
与 的函数关系式;
的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当 为何值时,△APR∽△PRQ?
为何值时,△APR∽△PRQ?
22.(本小题满分7分)
如下图,一次函数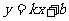 的图像与反比例函数
的图像与反比例函数 的图像相交于A、B两点。
的图像相交于A、B两点。
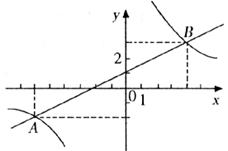
(1)根据图像,分别写出A、B的坐标;
(2)求出两函数解析式;
(3)根据图像回答:当 为何值时,一次函数值大于反比例数的函数值。
为何值时,一次函数值大于反比例数的函数值。
21.(本小题满分7分)
已知:如下图,在Rt△ABC 4中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A。

(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD︰AO=8︰5,BC=2,求BD的长。
20.(本小题满分6分)
某种子培育基地用A、B、C、D四种型号的小麦种子共2000粒进行发芽实验,从中选出发芽率高的种子进行推广,通过实验得知,C型号种子的发芽率为95%,根据实验数据绘制了图(1)和图(2)两幅尚不完整的统计图。

(1)D型号种子的粒数是__________。
(2)请你将图(2)的统计图补充完整;
(3)通过计算说明,应选哪一个型号的种子进行推广;
(4)若将所有已发芽的种子放到一起,从中随机取一粒,求取到B型号发芽种子的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com