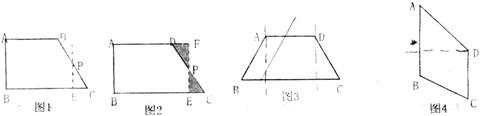
23．(本小题满分9分)如图1，在直角梯形ABCD中，AD∥BC，∠B=∠A=90°，AD=a，BC=b，AB=c，

示例操作：

我们可以取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，裁掉△PEC，并将△PEC拼接到△PFD的位置，构成新的图形(如图2)．

思考发现

小明在操作后发现，该剪拼方法就是先将△PEC绕点P逆时针旋转180°到△PFD的位置，易知PE与PF在同一条直线上。又因为在梯形ABCD中，AD∥BC，∠C+∠ADP=180°，则∠FDP+∠ADP=180°，所以AD和DF在同一条直线上。那么构成的新图形是一个四边形，进而根据平行四边形的判定方法，可以判断出四边形ABEF是一个平行四边形，而且还是一个特殊的平行四边形--矩形．

实践探究：

(1)矩形ABEF的面积是________；(用含a，b，c的式子表示)

(2)类比图2的剪拼方法，请你就图3和图4的两种情形分别画出剪拼成一个平行四边形的示意图．

联想拓展：

小明通过探究后发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．如图5的凸多边形中，AE=CD，AE∥CD，能否象上面剪切方法一样沿一条直线进行剪切，拼成一个平行四边形?若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．

22．(本小题满分8分)教师告诉同学们，可以用已知半径的球去测量圆柱形管子的内径，李明回家后把半径为5cm的小皮球置于保温杯的杯口上，经过思考找到了测量方法，问保温杯的内径是多少?

21．(本小题满分7分)某型号的摩托车油箱中的剩余油量Q(升)是它行驶的时间t(小时)的一次函数，小明骑摩托午外出，刚开始行驶时，油箱中有油8升，行驶了1小时后，他发现已耗油1.25升．

(1)求油箱中的剩余油量Q(升)与行驶的时间t(小时)的函数关系式，并求出自变量t的取值范围；

(2)在给定的直角坐标系中画出此函数的图象；

(3)从开始行驶时算起，如果摩托车以每小时50千米的速度匀速行驶，当油箱中的剩余油量为5.5升时，该摩托车行驶了多少千米？

19．(本小题满分6分)

解不等式组，并把解集在数轴上表示出来．

18．如图，在矩形ABCD中，AB=3，AD=4，P是AD上的动点，PE⊥AC于E，PF⊥BD于F，则PE+PF的值为________．

17．在△ABC中，∠A=30°，∠B=60°，AC=6，则△ABC的外接圆的半径为________．

16．从1，2，3，4四张卡片中任取两张，两张卡片上的数字之和为5的倍数的概率是________．

15．已知⊙O的直径是8，点O到直线a的距离为7，则直线a与⊙O位置关系是________．

14．如果点P(2-a，3a+1)在第二象限，那么a的取值范围是________．