
3.若长方形ABCD的邻边不等,分别以直线AB、BC为轴旋转一周得两个圆柱,观察这两个圆柱的底面和侧面,则有 ( ).
A.两个圆柱的底面积和侧面积都相等.
B.两个圆柱的底面积不相等,侧面积相等.
C.两个圆柱的底面积相等,侧面积不相等
D.两个圆柱的底面积与侧面积都不相等.
2.在一个底面半径为r厘米的圆柱形容器内,完全浸入一个圆锥,水面上升h厘米,这个圆锥体的体积是( )。
A. B.
B.
C. D.
D.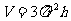
1.求加工一只无盖的圆柱形水桶所需铁皮的面积,就是求水桶的( )。
A.表面积 B.侧面积
C.底面积 D.侧面积与一个底面积之和
22. 正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,
(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM ∽Rt△AMN,求此时x的值.

21.小明用下面的方法求出方程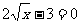 的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
的解,请你仿照他的方法求出下面另外两个方程的解,并把你的解答过程填写在下面的表格中.
|
方程 |
换元法得新方程 |
解新方程 |
检验 |
求原方程的解 |
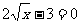 |
 |
 |
 |
  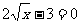 |
 |
|
|
|
|
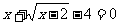 |
|
|
|
|
20.(1)如图1,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的 .
.
(2)如图2,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的 .
.

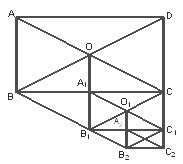
19.如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形 ,对角线相交于点
,对角线相交于点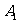 ;再以
;再以 为邻边作第2个平行四边形
为邻边作第2个平行四边形 ,对角线相交于点
,对角线相交于点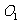 ;再以
;再以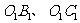 为邻边作第3个平行四边形
为邻边作第3个平行四边形 ……依此类推.
……依此类推.
(1)求矩形ABCD的面积;
(2)求第1个平行四边形 、第2个平行四边形
、第2个平行四边形  和第6个平行四边形的面积.
和第6个平行四边形的面积.
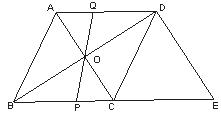
18.在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E.
(1)求△BDE的周长;
(2)点P为线段BC上的点,连接PO并延长交AD于点Q.求证:BP=DQ.
17.某中学学生会为了解该校学生喜欢球类活动的情况,采取抽样调查地方法,从足球、乒乓球、篮球、排球等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制成如下的两幅不完整的统计图(如图1、图2,要求每位同学只能选择一种自己喜欢的球类;图中用乒乓球、足球、排球、篮球代表喜欢这四种球类中的某一种球类的学生人数),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少位学生?
(2)喜欢排球的人数在扇形统计图中所占的圆心角是多少度?
(3)补全频数分布折线统计图.


16.某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮被感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com