
1.分式 中的
中的 同时扩大2倍,则分式的值
同时扩大2倍,则分式的值
A.不变 B.扩大2倍 C.扩大4倍 D.是原来的
26.(本小题满分9分)
已知抛物线 ,其中
,其中 ,b,c分别是△ABC中∠A,∠B,∠C的对边.
,b,c分别是△ABC中∠A,∠B,∠C的对边.
(1)求证:该抛物线与 轴必有两个交点;
轴必有两个交点;
(2)设抛物线与 轴的两个交点为P,Q,顶点为R,∠PQR=
轴的两个交点为P,Q,顶点为R,∠PQR= ,已知
,已知 ,△ABC的周长为10,求抛物线的解析式;
,△ABC的周长为10,求抛物线的解析式;
(3)设直线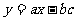 与抛物线交于点E,F,与
与抛物线交于点E,F,与 轴交于点M;抛物线与
轴交于点M;抛物线与 轴交于点N.若抛物线的对称轴为直线
轴交于点N.若抛物线的对称轴为直线 ,△MNE与△MNF的面积之比为5:1,试判断△ABC的形状,并证明你的结论.
,△MNE与△MNF的面积之比为5:1,试判断△ABC的形状,并证明你的结论.
24.(本小题满分7分)
我市荣县某水果批发市场,荔枝的价格如下表:
|
购买荔枝数量(kg) |
不超过20
kg |
20 kg以上但不超过40kg |
40kg以上 |
|
每千克价格 |
6元 |
5元 |
4元 |
张阿姨分两次购买荔枝共50 kg(第二次多于第一次),共付款264元,请问:张阿姨第一次,第二次各购买荔枝多少千克?
23.(本小题满分7分)
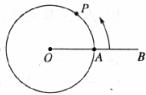
如图,点A是半径为6 cm的⊙O上的一个定点,动点P从点A出发,以 cm/s的速度沿圆周逆时针运动。当P回到点A立即停止运动.
cm/s的速度沿圆周逆时针运动。当P回到点A立即停止运动.
(1)若∠POA=90°,求点P运动的时间;
(2)延长OA至B,使AB=OA,当点P运动的时间为2 s时,判断直线BP与⊙O的位置关系,并说明理由.
22.(本小题满分6分)
围棋盒中有 颗白色棋子,
颗白色棋子, 颗黑色棋子,从盒中随机地取出一个棋子,若它是白色棋子的概率是
颗黑色棋子,从盒中随机地取出一个棋子,若它是白色棋子的概率是 ,
,
(1)试写出 与
与 的函数关系;
的函数关系;
(2)第一次取出的棋子放回盒中,再往盒中放入6颗白色棋子,若随机取出一颗白色棋子的概率为 ,求
,求 和y的值.
和y的值.
21.(本小题满分6分)
如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B’处,点A落在A’处.
(1)求证:B’E=BF;
(2)设AE= ,AB=b,BF=c,
,AB=b,BF=c,
试猜想 、b、c之间有何等量关系,并给予说明.
、b、c之间有何等量关系,并给予说明.

20.(本小题满分6分)
如图,在梯形ABCD中,CD//AB,AB=2,BC=3,CD=1,E是AD的中点,求证:CE⊥BE.

19.(本小题满分5分)
如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转的最小角度是多少度?
(3)若M是AB的中点,那么经过上述旋转后,点M转到了什么位置?

18.(本小题满分5分)
解方程: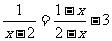
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com