
26.如图,正方形ABCO的边长为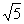 ,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转
,以O为原点建立平面直角坐标系,点A在x轴的负半轴上,点C在y轴的正半轴上,把正方形ABCO绕点O顺时针旋转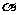 后得到正方形A1B1ClO(
后得到正方形A1B1ClO(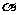 <450),BlCl交Y轴于点D,且D为BlCl的中点,抛物线y=ax2+bx+c过点Al、Bl、Cl
<450),BlCl交Y轴于点D,且D为BlCl的中点,抛物线y=ax2+bx+c过点Al、Bl、Cl
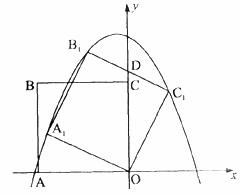
(1)求tan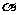 的值;
的值;
(2)求点A1的坐标,并直接写出点B1、点C1的坐标;
(3)求抛物线的函数表达式及其对称轴;
(4)在抛物线的对称轴上是否存在点P,使△PB1C1为直角三角形,若存在,直接写出所有满足条件的P点坐标;若不存在,请说明理由.
25.如图l,P是线段AB上的一点,在AB的同侧作AAPC和ABPD,使∠APC=∠BPD,PC=PA,PD=PB,连接CD,点E、F、C、H分别是AC、AB、BD、CD的中点,顺次连接E、F、G、H.

(1)猜想四边形EFGH的形状,直接回答,不必说明理由;
(2)当点P在线段AB的上方时,如图2,在△APB的外部作△APC和ABPD,其它条件不变,(1)中结论还成立吗?说明理由;
(3)如果(2)中,∠APC=∠BPD=900,其它条件不变,先补全图3.再判断四边形EFGH的形状,并说明理由.
24.面对国际会融危机,某铁路旅行社为吸引市民组圆去某风景区旅游,现推出如下标准:
|
人 数 |
不超过25人 |
超过25人但不超过50人 |
超过50人 |
|
人均旅游费 |
1500元 |
每增加1人,人均旅游费降低20元 |
1000元 |
某单位组织员工去该风景区旅游,设有x人参加,应付旅游费y元.
(1)请写出y与x的函数关系式;
(2)若该单位现有45人,本次旅游至少去26人,则该单位最多应付旅游费多少元?
23.“五一”假期小明骑自行车去郊游,早上8:00从家出发,9:30到达目的地,在郊游地点玩了3个半小时后按原路以原速返回,同时爸爸骑电动车从家出发沿同一路线迎接他,爸爸骑电动车的速度是20千米/小时,小明骑自行车的速度是l0千米/小时.设小明离开家x小时,下图是他们和家的距离y(千米)与x(时)的函数关系图象.
(1)目的地与家相距_______千米;
(2)设爸爸与家的距离为y1(千米),求爸爸从出发到与小明相遇的过程中。y1与x的函数关系式(不要求写出自变量石的取值范围);
(3)设小明与家的距离为y2(千米),求小明从返程到与爸爸相遇的过程中,y2与x的函数关系式(不要求写出自变量戈的取值范围);
(4)说明点C的实际意义,并求出此时小明与家的距离
22.如图,已知△ABC,∠C=∠ABC,以AB为直径作⊙O交BC于D,DE上AC,垂足为E.

(1)判断DE与⊙O的位置关系,并说明理由;
(2)如果BC=10.CE=4,求直径AB的长.
21.为了预防甲型H1N1流感,广东某口罩加工厂承担了加工24000个新型防病毒口罩的任务,由于时间紧急,实际加工时每天的工作效率比原计划提高了50%,结果提前5天完成任务,该厂实际每天加工这种口罩多少个?
20.哥哥和弟弟都是奥运迷,哥哥手中有四张奥运福娃卡片,如图,其中一张贝贝,一张晶晶,两张欢欢,除正面的图案不同外,其余都相同,将这四张卡片背面朝上洗匀后再从中随机抽取.

(1)弟弟从中抽取一张卡片是欢欢的概率是多少?
(2)弟弟一次抽取两张卡_片都是欢欢的概率是多少?(用树状图或列表法解答)
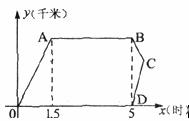
19.我市团委要为灾区某中学捐赠书籍,为了了解学生的喜好,随机抽取该校若干名学生进行问卷调查(每人只选一种),下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)这次活动一共调查了多少名学生?
(2)在扇形统计图中,求“其他”所在扇形的圆心角的度数;
(3)将两幅统计图补充完整;
(4)如果全校有1200名学生,请你估计全校喜欢“科幻”的学生人数.
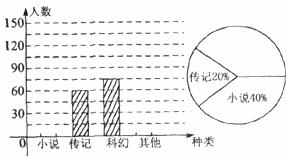
18.如图,在所给网格中完成下列各题:
(1)画出图1关于直线MN对称的图2;
(2)从平移的角度看,图2是由图l向________平移_______个单位得到的;
(3)画出图1绕点P逆时针方向旋转900后的图3.
17.解不等式组,并把解集在数轴上表示出来.
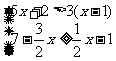
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com