22．如图，在平面直角坐标系中，点C(-3，0)，点A、B分别在轴、轴的正半轴上，且满足．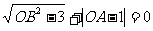

(1)求点A、点B的坐标．

(2)若点P从C点出发，以每秒1个单位的速度沿射线CB运动，连结AP．设△ABP的面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围．

(3)在(2)的条件下，是否存在点P，使以点A、B、P为顶点的三角形与△AOB相似?若存在，请直接写出点P的坐标；若不存在，请说明理由．

21．如图(1)、(2)、(3)、…、()，M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正边形ABCDE…的边AB、BC上的点，且BM=CN，连结OM、ON．

(1)求图(1)中∠MON的度数．

(2)图(2)中∠MON度数是 _______，图(3)中∠MON的度数是__________．

(3)试探究∠MON的度数与正边形边数的关系(直接写出答案)．

20．某中学新建了一栋4层的教学大楼，每层楼有8间教室，进出这栋大楼共有4道门，其中两道正门大小相同，两道侧门大小也相同．安全检查中，对4道门进行了测试：当同时开启一道正门和两道侧门时，2分钟内可以通过560名学生；当同时开启一道正门和一道侧门时，4分钟内可以通过800名学生．

(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生．

(2)检查中发现，紧急情况时因学生拥挤，出门的效率将降低20%．安全检查规定：在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离．假设这栋教学大楼每间教室最多有45名学生，问：建造的这4道门是否符合安全规定?请说明理由。

19．四川汶川大地震牵动了侨乡人民的心，全市广大中学生纷纷伸出了援助之手，为抗震救灾踊跃捐款．市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查，得到了一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各长方形的高度之比为3：4：5：8：6，又知此次调查中捐款25元和30元的学生一共42人．

(1)他们一共调查了多少人?

(2)这组数据的众数、中位数各是多少?

(3)若该校共有1560名学生，估计全校学生捐款多少元?

18．如图，已知在Rt△ABC中，∠C=90⁰，AD是∠BAC的角平分线，以AB上一点。为圆心，AD为弦作⊙O．

(1)在图中作出⊙O．(不写作法，保留作图痕迹)

(2)求证：BC为⊙O 的切线．

17．在直角坐标系内，一次函数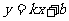的图象经过点A(2，0)、B(0，2)、C(m，3)，求这个一次函数的解析式，并求m的值．

16．如图，某幢大楼顶部有一块广告牌CD，甲乙两人分别在相距8米的A、B两处测得D点和C点的仰角分别为45⁰和60⁰，且A、B、E三点在一条直线上，若BE=15米，求这块广告牌的高度．(取≈l．73，计算结果保留整数)

15．已知关于的一元二次方程．

请你为m选取一个合适的整数，使得到的方程有两个不相等的实数根．

14．解不等式组并把解集在数轴上表示出来

13．如图，有一个直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，请你求出CD的长．