28.　（本小题满分12分）已知：如图1所示，直线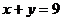与x轴、y轴相交于C、D两点，直线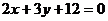与x轴、y轴相交于A、B两点，F（4,0）是x 轴上一点，过C点的直线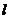垂直于x轴，N是直线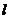上一点（N点与C点不重合），连结AN.

（1）求A、D两点的坐标；

（2）若P是AN的中点，PF＝5，猜想∠APF的度数，并说明理由.

（3）如图2所示，连结NF，求△ AFN外接圆面积的最小值，并求△AFN外接圆面积最小时，圆心G的坐标.

27.　（本小题满分12分）如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP．

（1）在图1中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；

（2）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连结AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；

（3）将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连结AP，BQ．你认为（2）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．

26.　（本小题满分10分）如图，矩形ABCD的长、宽分别为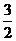和1，且OB＝1，点E，连结AE、ED.

（1）求经过A、E、D三点的抛物线的表达式；

（2）若以原点为位似中心，将五边形AEDCB放大，使放大后的五边形的边长是原五边形对应边长的3倍，请在下图网格中画出放大后的五边形A′E′D′C′B′；

（3）经过A′、E′、D′三点的抛物线能否由（1）中的抛物线平移得到？请说明理由.

25.　（本小题满分10分）码头工人往一艘轮船上装载货物，装完货物所需的时间y（分钟）与装载速度x（吨/分钟）之间满足反比例函数关系，图象如图所示.

（1）这批货物的质量是多少？

（2）若b－c＝40（分钟），请根据图中提供的信息求b、c、d的值.

（3）在（2）的条件下，若轮船到达目的地后，以d（吨/分钟）的速度开始装货，装到一半时，一辆吊车发生故障，因而每分钟少装1吨,那么装满这船货物一共需要多少时间？

24.　（本小题满分10分）商场正在销售 “福娃”玩具和徽章两种奥运商品，已知购买1盒“福娃”玩具和2盒徽章共需145元；购买2盒“福娃”玩具和3盒徽章共需280元.

（1）一盒“福娃”玩具和一盒徽章的价格各是多少元？

（2）某公司准备购买这两种奥运商品共20盒送给幼儿园（要求每种商品都要购买），且购买总金额不能超过450元，请你帮公司设计购买方案.

（2）当∠D＝30°，BC＝1时，求圆中阴影部分的面积（π≈3.14，≈1.73，结果精确到十分位）