P() = ×× = 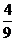, P() = ×× =  .

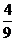          表示事件“一个实验组中, 服用B有效的小白鼠有j只”, j = 0,1,2 .

依题意有

    (Ⅰ) 设表示事件“一个实验组中, 服用A有效的小白鼠有i只”, i=0,1,2,

    由于事件,,互斥, 事件,相互独立, 根据乘法法则和加法法则便可得题目要求的概率.

    第(Ⅱ)问. 观察3个实验组可视为3次独立重复试验, 由此可得解. 具体求解如下.

    第(Ⅰ)问. 事件“一个试验组为甲类组”(记为D)可分解为: 事件“服用A有效的小白鼠为1只且服用B有效的小白鼠为0只”(记为)、事件“服用A有效的小白鼠为2只且服用B有效的小白鼠为0只”(记为)、事件“服用A有效的小白鼠为2只且服用B有效的小白鼠为1只”(记为)之和, 而上述三事件又可分解为事件“服用A有效的小白鼠为i只”(记为)与事件“服用B有效的小白鼠为j只”(记为)之交, 其中i=1,2; 0≤j＜i. 而一个组内两只小白鼠服用A(或B)是否有效可视为2次独立重复试验.

   0.24

    从答题情况看本题属于难题, 未得分者有五成之多. 不过区分度很好. 不少的人对将问题化为用概率语言符号表示不熟练, 卷面上经常见到一长串的数字算式, 没有必要的语言叙述. 第(Ⅰ)问中, 不会将两只小白鼠服用A(或B)视为2次独立重复试验, 公式运用不准确错得结果5/18者较多, 这种情况一般得分在4~6分, 有约24%. 得分超过7分即第(Ⅰ)问答对者近16%. 完整解答本题的有11%.

    [考查意图] 主要考查计算随机事件发生的概率, 包括互斥事件有一个发生的概率、对立事件有一个发生的概率、相互独立事件有一个发生的概率以及n次独立重复试验中某事件恰好发生k次的概率, 同时考查运用概率知识解决实际问题的能力.

    [解答分析] 求解时, 首先需仔细理解题意, 正确地将复杂事件分解为一些简单事件的复合, 然后合理地列式计算.

   2.83

    A、B 是治疗同一种疾病的两种药, 用若干试验组进行对比试验. 每个试验组由4只小白鼠组成, 其中2只服用A, 另2只服用B, 然后观察疗效. 若在一个试验组中, 服用A有效的小白鼠的只数比服用B有效的多, 就称该试验组为甲类组. 设每只小白鼠服用A有效的概率为 , 服用B有效的概率为.

    (Ⅰ) 求一个试验组为甲类组的概率;

    (Ⅱ) 观察3个试验组, 求这3个试验组中至少有一个甲类组的概率.

    [抽样统计数据]

题号

满分

  平均分

   难度

  文(19)

    12

    (3) 记错三角公式, 记错特殊角的三角函数. 如: 将 错写为; 将= 错写为 =; 在推出=后, 有的求不出A的值, 有的错为A =  或 A =  等.

    [复习提示] 三角函数的基本公式、图象与性质、特殊角的三角函数等基本知识应烂熟于心. 注意三角函数式的化简训练. 三角函数式的变形化简需首先根据要求确定化简目标, 然后选择适当的途径, 根据目标进行恒等变形转化.

文(19) (本小题满分12分)

有的错为:－2+ , －2,…等等多种多样的情形.