正确的表达式应为 p =×× .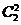

    (3) 逻辑关系不清楚造成失误. 如将“最多有3个不是甲类组”当成“3个试验组中至少有一个甲类组”的对立事件.

    另外, 数字运算错误, 求解中考虑情况不周全, 也是不少考生失分的原因.

    [复习提示] 概率的计算问题, 列出算式后的计算并不难, 重要地是如何列式进行计算? 这就需要分清问题属于哪种类型的概率问题? 使用什么公式列式? 需要正确地将复杂事件分解为简单事件的复合.

理（18）（本小题满分12分）

(2) 未审清题目或未正确理解题意造成失误. 如有的考生在解题中, 还考虑一个试验组中服用A有效的小白鼠为3只或4只的情况, 忽视了题设条件. 又如有的考生计算一个试验组中,服用A有效的小白鼠有2只的概率时, 列式为p = 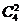××, 误解了题意, 而将一个试验组中, 服用A的2只小白鼠的所有可能选法都考虑了进去. 根据题意, 一个试验组中, 斤2只小白鼠服用A, 另2只服用B, 观察疗效, 那么服用A有效的为2只就只有一种情况,

(1) 概念不清, 公式运用不准确造成失误. 如计算事件“服用A有效的小白鼠为1只, 服用B有效的小白鼠为0只”的概率, 把式子列为 p = ××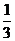×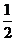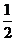= 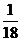, 误在丢掉了因子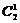. 实际上, 因为有2只小白鼠服用A, 所以“服用A有效的小白鼠有1只”的概率, 即为“2次独立重复试验中一事件恰好发生1次”的概率, 应为×× .

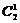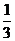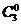
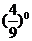
所以, 所求的概率为p 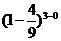= 1－= 1－=  .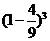

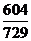    这里也可以用直接法来做, 但相比之下间接法较简捷.

    [错因分析]

(Ⅱ) 事件“三个试验组中至少有一个甲类组”的对立事件为“三个试验组中恰好有0个甲类组”, 后一事件的概率为.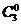

                =  .

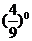
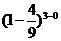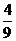    这种算法可称为直接法, 本题也可用间接法即通过计算“一个试验组为甲类组”的对立事件的概率来求解, 但因情况较多, 较为复杂.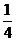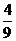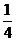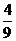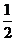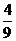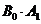

                = ×+×+×

                = P() + P(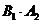) + P()

              p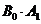 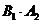= P(++)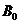

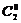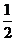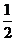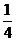              P() = ×× = , P() = ×× =  .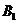

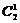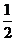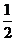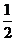    所求的概率为