
 ,即
,即  ,
,
解 (Ⅰ) 焦点在y轴上,故设椭圆方程为  ,(
,( ),由题设条件得,
),由题设条件得, 且
且 ,即b=2,a =1,所以曲线C的方程为
,即b=2,a =1,所以曲线C的方程为
本小题属于中等题, 区分度较好.得0分者约占18%, 会求椭圆方程得1~4分者有约50%, 会求导数和切线斜率得5~6分者有10.5%, 正确求出切线方程以及进一步求解点M的轨迹方程得7~10分者有16%, 做到第(Ⅱ)问得11~12分者有5.5%.
[考查意图] 本小题主要考查椭圆的几何性质、平面向量及切线方程、曲线方程等基本知识,考查综合运用数学知识解决问题及推理的能力.
[解答分析] 本小题第(Ⅰ) 问涉及到解析几何、平面向量和导数应用等多方面知识,同时出现椭圆方程、切线方程和点M的轨迹方程等多个方程,因此做第(Ⅰ)问需要我们清楚理解方程等有关的概念,熟练掌握有关的基本知识、常规方法,并能把他们联系在一起综合的运用. 解题思路是:设出切点P的坐标和M点坐标,求出椭圆方程和切线方程,然后求出A、B点坐标,再求出M点坐标与切点坐标的关系,消去切点坐标即可得点M的轨迹方程. 做第(Ⅱ)问需要一点运算技巧. 参考解答如下:
0.32
3.88
(Ⅰ) 点M的轨迹方程; (Ⅱ)  的最小值.
的最小值.
[抽样统计数据]
题号
满分
平均分
难度
理(20)
12
在平面直角坐标系xOy中, 有一个以F1(0,
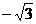 ) 和F2(0,
) 和F2(0,
 )为焦点、离心率为
)为焦点、离心率为 的椭圆. 设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x、y轴的交点分别为A、B, 且向量
的椭圆. 设椭圆在第一象限的部分为曲线C, 动点P在C上, C在点P处的切线与x、y轴的交点分别为A、B, 且向量  . 求:
. 求:
(Ⅱ)∵ =(1,1,m), =(-1,1,m), ∴||=||, 又已知∠ACB=60°,∴△ABC为正三角形,AC=BC=AB=2.
在Rt△CNB中,NB=, 可得NC=,故C(0,1, ).
连结MC,作NH⊥MC于H,设H(0,λ, λ) (λ>0).
∴=(0,1-λ,-λ), =(0,1, ). ? = 1-λ-2λ=0, ∴λ= ,
∴H(0, , ), 可得=(0,, - ), 连结BH,则=(-1,, ),
∵?=0+ - =0, ∴⊥, 又MC∩BH=H,∴HN⊥平面ABC,
∠NBH为NB与平面ABC所成的角.又=(-1,1,0),
∴cos∠NBH= = = .
注:还可以分别以NA、NB、NC为x、y、z轴建立空间直角坐标系,但这需要先证明
l2⊥平面ABN.
[错因分析] 缺少解答步骤:主要是在第(Ⅰ) 问中不证明l2⊥平面ABN,在第(Ⅱ)问中不证明△ABC为正三角形或NC=NA=NB,或不证明∠NBH是所求的线面角,而是默认它们成立.
不按照题意回答问题:算出∠NBH的大小(用反三角函数表示),但不算它的余弦值.
线面角的概念不清楚:例如说“∠NBH或其补角是所求的线面角”.
找不到所求的线面角,或是按照定义作出了∠NBH,但是找不到H的位置,因而无法计算∠NBH的余弦值.
找错所求的线面角:例如把平面ABC的法向量与NB的夹角,说所求的线面角是∠NMC,是∠NBC,是∠MNB,是∠DBN(D为BC中点),是∠DME (D为BC中点,E为BN中点),等等.
计算错误:向量内积算错,列式运算错,线段长度看错等.
空间想象能力弱:如说“过B作BE∥AC交l2于E”,其实这是不可能相交的.
[复习提示] 在解答立体几何题时,常有考生缺少证明步骤,比如本小题不证明l2⊥平面ABN,其实这一步并不难,但是不写的话失分就较多. 在高考复习时,要注意练习写一个既简明又完整的解答或证明,哪些是必不可少的,那些是可以省略的,这从课本例题、老师讲的例题的解答中就可以学到.
理(20)(本小题满分12分)
 在Rt△NHB中,cos∠NBH= = = .
在Rt△NHB中,cos∠NBH= = = .
解法二: 如图,建立空间直角坐标系M-xyz. 令MN=1, 则有A(-1,0,0),B(1,0,0),N(0,1,0),
(Ⅰ) ∵MN是 l1、l2的公垂线, l1⊥l2,
∴ l2⊥平面ABN. ∴ l2平行于z轴.
故可设C(0,1,m),于是 =(1,1,m), =(1,-1,0).
∵ ?=1+(-1)+0=0 ∴AC⊥NB.
 参考解答如下:
参考解答如下:
解法一: (Ⅰ) 由已知MN⊥l1 , AM=MB=MN,可知AN=NB且AN⊥NB.
又由已知l2⊥MN, l2⊥l1 , MN∩l1 =M, 可得l2⊥平面ABN,
从而AN为AC在平面ABN内的射影. ∴AC⊥NB
(Ⅱ)∵ Rt△CNA≌Rt△CNB,
∴AC=BC,又已知∠ACB=60°,因此△ABC为正三角形.
∵Rt△ANB≌Rt△CNB, ∴NC=NA=NB,因此N在平面ABC内的射影H是正三角形ABC的中心,连结BH,∠NBH为NB与平面ABC所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com